
����Ŀ����ͼ���ڵȱ�������ABC����BC=6cm. ����AG//BC����E�ӵ�A����������AG��1cm/s���ٶ��˶���ͬʱ��F�ӵ�B����������BC��2cm/s���ٶ��˶������˶�ʱ��Ϊt(s) ��
��1������EF����EF����AC�ߵ��е�Dʱ����֤����ADE�ա�CDF��
(2)��tΪ��ֵʱ���ı���ACFE��������
��3���Ƿ����ijһʱ��t��ʹ��A��F��C��EΪ������ı����ڽdz���ֱ�ǣ������ڣ����t��ֵ���������ڣ���˵��������
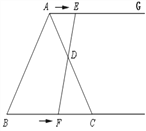
���𰸡���1��֤���������� (2)t=6�� ��3�����ڣ����ɼ�������
����������������1��������õ�AD=CD������AG��BCƽ�У�������ֱ��ƽ���ڴ�����ȵõ����Խ���ȣ�����AAS���ɵ�֤����2�����ı���ACFE�����Σ�����CF=AC=AE=6����E���ٶ����E�˶���ʱ�伴�ɣ���3��������������ǣ���CE��AG����ʱ�ĵ㹹�������Σ�����ֱ�����Σ���AF��BC�����BF�ij��ȼ�ʱ��t��ֵ��
�����������1�� ֤������AG��BC ,��![]() ,��
,��![]() ��AC�ߵ�,��AD=CD
��AC�ߵ�,��AD=CD
�֡�![]() , ���ADE�ա�CDF
, ���ADE�ա�CDF
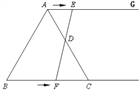
��2���ߵ��ı���ACFE������ʱ����AE=AC=CF=EF,
�������֪��AE=t,CF=2T-6����t=6,
��3�����ı����ڽ���ֱ��ʱ����������������ı���ACFE��ֱ�����Σ���ʱEF��AG�� ��![]() ��CM��AG��M��AM=3���Եõ�AE-CF=AM��
��CM��AG��M��AM=3���Եõ�AE-CF=AM��
��t-(2t-6)=3,��t=3��
��ʱ��C��F�غϣ����������⣬��ȥ��
���ı���![]() ��ֱ�����Σ���ʱAF��BC��
��ֱ�����Σ���ʱAF��BC��
�ߡ�ABC�ǵȱ������Σ�F��BC�е㣬
��2t=3�������飬�������⣬��t=![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
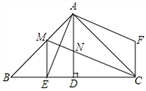
����Ŀ����ͼ��![]() �У�
�У�![]() ������D��AEƽ��
������D��AEƽ��![]() ����BC�ڵ�E����
����BC�ڵ�E����![]() ����һ��F��ʹ
����һ��F��ʹ![]() .
.
��1�����ACF�Ķ�����
��2����֤��![]() ��
��
��3����AB��ȡһ��M��ʹ![]() ������MC����AD�ڵ�N������ME.��֤��
������MC����AD�ڵ�N������ME.��֤��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BDΪ��ABC�Ľ�ƽ���ߣ���BD=BC��EΪBD���ӳ����ϵ�һ�㣬BE=BA����E��EF��AB��FΪ���㣬���н��ۣ��١�ABE=��ACE���ڡ�BCE+��BCD=180������AE=EC����BE+BD=2BF��������ȷ���ǣ�����

A. �٢ڢ� B. �٢ۢ� C. �٢ڢ� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
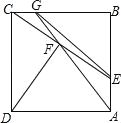
����Ŀ����ͼ����������ABCD�У���EΪ��AB����һ�㣨���A��B���غϣ�������CE������D��DF��CE�ڵ�F������AF���ӳ���BC���ڵ�G������EG���������α߳�Ϊ4��GC=![]() AE����GE= ��
AE����GE= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������������ÿ̨���۷ֱ�Ϊ200Ԫ��170Ԫ��A��B�����ͺŵĵ���ȣ������ǽ����ܵ����������
����ʱ�� | �������� | �������� | |
A���ͺ� | B���ͺ� | ||
��һ�� | 3̨ | 5̨ | 1800Ԫ |
�ڶ��� | 4̨ | 10̨ | 3100Ԫ |
�����ۡ��ۼ۾����ֲ��䣬����=�������멁�����ɱ���
��1����A��B�����ͺŵĵ���ȵ����۵��ۣ�
��2�����������ò�����5400Ԫ�Ľ���ٲɹ��������ͺŵĵ���ȹ�30̨����A���ͺŵĵ��������ܲɹ�����̨��
��3���ڣ�2���������£�������������30̨������ܷ�ʵ������Ϊ1400Ԫ��Ŀ�ꣿ���ܣ��������Ӧ�IJɹ������������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��P��2m+4��m��1�����Էֱ�������������������P�����꣮
��1����P��y���ϣ�
��2����P��������Ⱥ������3��
��3����P�ڹ�A��2����4���㣬����x��ƽ�е�ֱ���ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒ���˶����������ν��ۣ�ÿ�����ۼ���560Ԫ��Ϊ315Ԫ����֪���ν��۵İٷ�����ͬ����ÿ�ν��۵İٷ��ʣ���ÿ�ν��۵İٷ���Ϊx���������еķ�������ȷ���ǣ� ��
A.560��1+x��2=315
B.560��1��x��2=315
C.560��1��2x��2=315
D.560��1��x2��=315
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����50�����ݷֳ����飬������Ϊ�����ݵ�����飬Ƶ���䲼���±���
��� | �� | �� | �� | �� | �� |
Ƶ�� | 8 | 10 | �� | 14 | 11 |
��ô�ڢ����Ƶ��Ϊ��������
A. 14 B. 7 C. 0.14 D. 0.7
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com