
����Ŀ����ͼ���ڵȱ�������ABC�У���D��E�ֱ��ڱ�AB��AC�ϣ�AD=AE������BE��CD����M��N��P�ֱ���BE��CD��BC���е㣬����DE��PM��PN��MN��
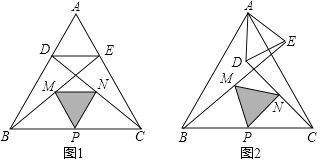
��1���۲���룬��ͼ����PMN��_______�������������ε����ƣ�
��2��̽��֤������ͼ����ADE�Ƶ�A����ʱ�뷽����ת������PMN����״�Ƿ����ı䣿������ͼ˵�����ɣ�
��3����չ���죬����ADE�Ƶ�A��ƽ����������ת��AD=2��AB=6����ֱ��д����PMN���ܳ������ֵ��
���𰸡���1���ȱ������Σ���2��![]() ����״�������ı䣬��Ϊ�ȱ������Σ����ɼ���������3��
����״�������ı䣬��Ϊ�ȱ������Σ����ɼ���������3��![]() ���ܳ������ֵΪ12
���ܳ������ֵΪ12
��������
��1����ͼ1���ȸ��ݵȱ������ε����ʵõ�AB=AC����ABC=��ACB=60������BD=CE���ٸ�����������λ�����ʵ�PM��CE��PM![]() CE��PN��AD��PN
CE��PN��AD��PN![]() BD���Ӷ��õ�PM=PN����MPN=60�����Ӷ����ж���PMNΪ�ȱ������Σ�
BD���Ӷ��õ�PM=PN����MPN=60�����Ӷ����ж���PMNΪ�ȱ������Σ�
��2������CE��BD����ͼ2���ȸ�����ת�����ʵõ���ABD����ACE����BD=CE����ABD=��ACE��Ȼ��ɵ�PM=PN�������MPN=60�������ǿ��ж���PMNΪ�ȱ������Σ�
��3������AB��AD��BD��AB+AD�����ҽ�����B��A��D����ʱȡ�Ⱥţ��õ�BD�����ֵΪ8����PN�����ֵΪ4��Ȼ���ȷ����PMN���ܳ������ֵ��
��1���ȱ������Σ��������£�
��ͼ1��
�ߡ�ABCΪ�ȱ������Σ���AB=AC����ABC=��ACB=60����
��AD=AE����BD=CE��
�ߵ�M��N��P�ֱ���BE��CD��BC���е㣬��PM��CE��PM![]() CE��PN��AD��PN
CE��PN��AD��PN![]() BD����PM=PN����BPM=��BCA=60������CPN=��CBA=60�������MPN=60�������PMNΪ�ȱ������Σ�
BD����PM=PN����BPM=��BCA=60������CPN=��CBA=60�������MPN=60�������PMNΪ�ȱ������Σ�
�ʴ�Ϊ���ȱ������Σ�
��2����PMN����״�������ı䣬��Ϊ�ȱ������Σ��������£�
����BD��CE������ת�ɵá�BAD=��CAE��
����ABC�ǵȱ������Σ���AB=AC����ACB=��ABC=60����
�֡�AD=AE������ABD����ACE����BD=CE����ABD=��ACE��
��M��BE���е㣬P��BC���е㣬��PM����BCE����λ�ߣ���PM=![]() CE��PM//CE��
CE��PM//CE��
ͬ����֤PN=![]() BD��PN//BD����PM=PN����MPB=��ECB����NPC=��DBC
BD��PN//BD����PM=PN����MPB=��ECB����NPC=��DBC
���MPB+��NPC=��ECB+��DBC=����ACB+��ACE��+����ABC-��ABD��
=��ACB+��ABC=120�������MPN=60��������PMN�ǵȱ������Σ�
��3����PN![]() BD���൱BD��ֵ���ʱ��PN��ֵ���
BD���൱BD��ֵ���ʱ��PN��ֵ���
��AB��AD��BD��AB+AD�����ҽ�����B��A��D����ʱȡ�Ⱥţ�
��BD�����ֵΪ2+6=8����PN�����ֵΪ4�����PMN���ܳ������ֵΪ12��


 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д� â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���ABC��������������ֱ�ΪA��1��1����B��4��0����C��4��4����
��1��������Ҫ����ͼ��
�ٽ���ABC����ƽ��4����λ���õ���A1B1C1��
�ڽ���A1B1C1�Ƶ�B1��ʱ����ת90�㣬�õ���A2B2C2��
��2�����C1����ת��������������·������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��
��![]() �ᣬ
�ᣬ![]() ��ֱ��ڵ�
��ֱ��ڵ�![]() ��������
��������![]() ��������
��������![]() ��
��![]() �����һ������Ϊ��
�����һ������Ϊ��![]() ����
����![]() ����������һ�㣬����
����������һ�㣬����![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() �����
�����![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() .
.
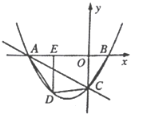
![]() �������ߵĽ���ʽ��
�������ߵĽ���ʽ��
![]() ����
����![]() �ڵ������ޣ���
�ڵ������ޣ���![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��
��![]() �ĺ�����ϵʽ�������
�ĺ�����ϵʽ�������![]() �����ֵ����ʱ��
�����ֵ����ʱ��![]() �����ꣻ
�����ꣻ
![]() ����
����![]() ����
����![]() ,��ֱ��д����ʱ��
,��ֱ��д����ʱ��![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʡ��Сѧ������չ�ۺ�ʵ�����ijУ����֯��չ�����ۺ�ʵ�������A.���Ƿ���С���ˣ�B.ѧ���ҳ��ͣ�C.���������ж���D.�Ҹ���λȥ������.Ϊ�˽�ѧ����ϲ�������ۺ�ʵ����������ȡ����ѧ�������ʾ����飨ÿλѧ��ֻ��ѡ��һ��������������Ƴ�����������������ͳ��ͼ������ͼ���ṩ����Ϣ�ش��������⣺
��1������һ�������� ��ѧ����������ͳ��ͼ�У�m��ֵ�� ��
��2����ȫ����ͳ��ͼ��
��3������У����1200��ѧ����������ϲ��B��C��Ŀ��ѧ��һ���ж�������
��4��������ϲ��A��B��C��D���Ŀ��ѧ����һ�ˣ�ѧУҪ�������������ѡȡ���˽������ᣬ�����б�����״ͼ�ķ������ǡ��ѡȡ��ϲ��C��D��Ŀ����λѧ���ĸ���.
��ϲ�������ۺ�ʵ�������ͳ��ͼ ��ϲ�������ۺ�ʵ�������ͳ��ͼ


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ܡ����п������ؿ���Ŀ֮һ��������ij��ѧΪ���˽���꼶ѧ�������ܡ�������������ȡ���־��꼶ѧ�����Գɼ�������1000�ף�Ů��800�ף���������ʱ�䳤�����η�ΪA��B��C��D�ĸ��ȼ�����ͳ�ƣ�����������������������ͳ��ͼ������������Ϣ������������⣺
��1��������ͳ��ͼ�У�C��Ӧ������Բ�Ľ��� �ȣ�
��2����ȫ����ͳ��ͼ��
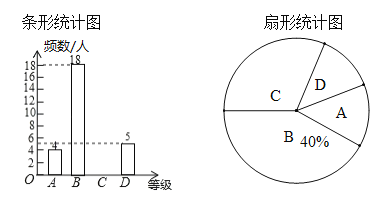
��3������ȡѧ���ġ����ܡ����Գɼ�����λ�������� �ȼ���
��4����У���꼶��675��ѧ��������ơ����ܡ����Գɼ��ﵽA����ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱ���ABC�У�PΪ��������һ�㣬��P��PD��BC��PE��AB��PF��AC������AP��BP��CP�����S��APF��S��BPE��S��PCD��![]() ����ô��ABC������Բ�뾶Ϊ___
����ô��ABC������Բ�뾶Ϊ___
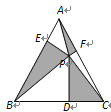
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2013��㶫÷��11�֣�����ͼ��������ʾ������ֱ�������Σ����ֱ߳����ǵĶ�����ͼ���ѱ�����������������̽�����⣺
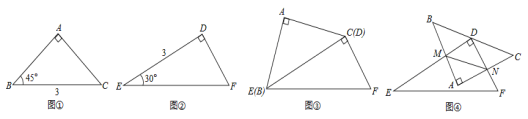
̽��һ��������������������ͼ��ƴ�ӣ�BC��ED�غϣ�����BC������һ����P��
��1������P�˶�����CFB�Ľ�ƽ������ʱ������AP�����߶�AP�ij���
��2������P���˶��Ĺ����г���PA=FCʱ������PAB�Ķ�����
̽��������ͼ��������DEF�Ķ���D������ABC��BC���ϵ��е㴦�����Ե�DΪ��ת������ת��DEF��ʹ��DEF����ֱ�DZ�����ABC����ֱ�DZ߷ֱ���M��N���㣬����MN������ת��DEF�Ĺ����У���AMN���ܳ��Ƿ��������Сֵ�������ڣ����������Сֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ������Ӧ��������ġ���ɫ��չ����̼���С����٣�ij������������һ���������������г�������֪������3����ʽ������4��Ůʽ����������ͬ������5����ʽ������4��Ůʽ��������16000Ԫ.
(1)����ʽ������Ůʽ�����ĵ��ۣ�
(2)������Ҫ����ʽ����Ůʽ������4�������ֵ���������Ҫ22�����������ֵ����ķ��ò�����50000Ԫ���������м��ֹ��÷������������ò���ʹ�����ܷ�����ͣ���ͷ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ÿ���6��5��Ϊ���绷���գ�Ϊ���ᳫ��̼������ij��˾��������10̨��ʡ��Դ�����豸�����мס��������ͺŵ��豸�ɹ�ѡ���������飺������3̨�����豸�ȹ���2̨�����豸���16��Ԫ������2̨�����豸�ȹ���3̨�����豸�ٻ�6��Ԫ.
��1����ס��������ͺ��豸�ļ۸�
��2���ù�˾��Ԥ����������ʡ��Դ�����豸���ʽ���110��Ԫ������Ϊ�ù�˾�м��ֹ�����
��3���ڣ�2���������£���֪�����豸�IJ���Ϊ240��/�£������豸�IJ���Ϊ180��/�£���ÿ��Ҫ���ܲ���������2040�֣�Ϊ�˽�Լ�ʽ�����Ϊ�ù�˾���һ����ʡǮ�Ĺ���.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com