
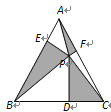
【题目】如图,等边△ABC中,P为三角形内一点,过P作PD⊥BC,PE⊥AB,PF⊥AC,连结AP、BP、CP,如果S△APF+S△BPE+S△PCD=![]() ,那么△ABC的内切圆半径为___
,那么△ABC的内切圆半径为___
【答案】![]()
【解析】
过P点作正△ABC的三边的平行线,可得△MPN,△OPQ,△RSP都是正三角形,四边形ASPM,四边形NCOP,四边形PQBR是平行四边形,则可得黑色部分的面积=白色部分的面积,进而求出三角形ABC的面积,然后求出等边三角形的边长和高,再根据等边三角形的内切圆的半径等于高的三分之一即可求出半径的长度.
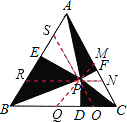
如图,过P点作正△ABC的三边的平行线,
则△MPN,△OPQ,△RSP都是正三角形,
四边形ASPM,四边形NCOP,四边形PQBR是平行四边形,
故可知黑色部分的面积=白色部分的面积,
∵S△APF+S△BPE+S△PCD=![]() ,
,
∴S△ABC=![]() ,
,
∵S△ABC=![]() AB2sin60°=
AB2sin60°=![]() ,
,
∴AB=6,
∴三角形ABC的高h=3![]() ,
,
则△ABC的内切圆半径r=![]() h=
h=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
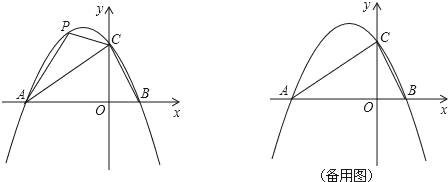
【题目】在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C.
(1)求这个二次函数的关系解析式;
(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由;
(3)在平面直角坐标系中,是否存在点Q,使△BCQ是以BC为腰的等腰直角三角形?若存在,直接写出点Q的坐标;若不存在,说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
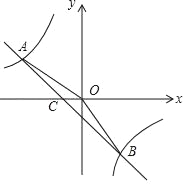
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于二象限内的A点和四象限内的B点,与x轴将于点C,连接AO,已知AO=2
的图象交于二象限内的A点和四象限内的B点,与x轴将于点C,连接AO,已知AO=2![]() ,tan∠AOC=
,tan∠AOC=![]() ,点B的坐标为(a,﹣4).
,点B的坐标为(a,﹣4).
(1)求此反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
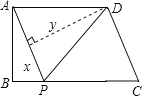
【题目】如图,四边形ABCD中,AD∥BC,∠ABC=90°,AB=3,AD=4,BC=![]() ,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )
,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )
A. 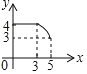 B.
B. 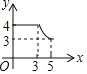
C. 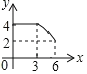 D.
D. 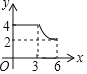
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点D,E分别在边AB,AC上,AD=AE,连接BE,CD,点M,N,P分别是BE,CD,BC的中点,连接DE,PM,PN,MN.
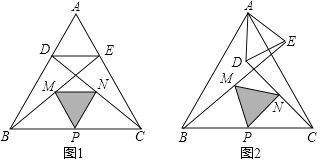
(1)观察猜想,如图中ΔPMN是_______(填特殊三角形的名称)
(2)探究证明,如图,ΔADE绕点A按逆时针方向旋转,则ΔPMN的形状是否发生改变?并就如图说明理由.
(3)拓展延伸,若ΔADE绕点A在平面内自由旋转,AD=2,AB=6,请直接写出ΔPMN的周长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租汽车公司有出租车100辆,平均每天每车消耗的汽油费为80元,为了减少环境污染,市场推出一种叫“CNG”的改烧汽油为天然汽的装置,每辆车改装价格为4000元.公司第一次改装了部分车辆后核算:已改装后的车辆每天的燃料费占剩下未改装车辆每天燃料费用的15%,公司第二次再改装同样多的车辆后,所有改装后的车辆每天的燃料费占剩下未改装车辆每天燃料费用的40%.问:
(1)公司共改装了多少辆出租车?改装后的每辆出租车平均每天的燃料费比改装前的燃料费下降了百分之多少?
(2)若公司一次性将全部出租车改装,多少天后就可以从节省的燃料费中收回成本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校积极参与垃圾分类活动,以班级为单位收集可回收的垃圾,下面是七年级各班一周收集的可回收垃圾的质量频数表和频数直方图(每组含前一个边界值,不含后一个边界值).
某校七年级各班一周收集的可回收垃圾的质量频数表
组别(kg) | 频数 |
4.0~4.5 | 2 |
4.5~5.0 | a |
5.0~5.5 | 3 |
5.5~6.0 | 1 |
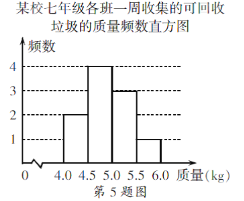
(1)求a的值;
(2)已知收集的可回收垃圾以0.8元/kg被回收,该年级这周收集的可回收垃圾被回收后所得的金额能否达到50元.
查看答案和解析>>
科目:初中数学 来源: 题型:
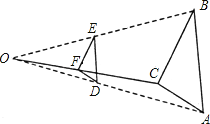
【题目】按如下方法,将△ABC的三边缩小的原来的![]() ,如图,任取一点O,连AO、BO、CO,并取它们的中点D、E、F,得△DEF,则下列说法正确的个数是( )
,如图,任取一点O,连AO、BO、CO,并取它们的中点D、E、F,得△DEF,则下列说法正确的个数是( )
①△ABC与△DEF是位似图形②△ABC与△DEF是相似图形
③△ABC与△DEF的周长比为1:2④△ABC与△DEF的面积比为4:1.
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
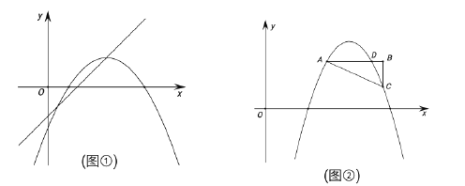
【题目】如图①,将抛物线![]() 平移到顶点恰好落在直线
平移到顶点恰好落在直线![]() 上,并设此时抛物线顶点的横坐标为
上,并设此时抛物线顶点的横坐标为![]() .
.
(1)求抛物线的解析式(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
(2)如图②,![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 、
、![]() 三点,
三点,![]() ,
,![]() 轴,
轴,![]() ,
,![]() .
.
①求![]() 的面积(用含
的面积(用含![]() 的代数式表示);
的代数式表示);
②若![]() 的面积为1,当
的面积为1,当![]() 时,
时,![]() 的最大值为-3,求
的最大值为-3,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com