
【题目】如图①,将抛物线![]() 平移到顶点恰好落在直线
平移到顶点恰好落在直线![]() 上,并设此时抛物线顶点的横坐标为
上,并设此时抛物线顶点的横坐标为![]() .
.
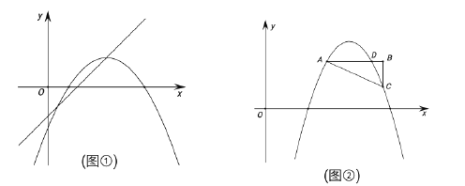
(1)求抛物线的解析式(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
(2)如图②,![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 、
、![]() 三点,
三点,![]() ,
,![]() 轴,
轴,![]() ,
,![]() .
.
①求![]() 的面积(用含
的面积(用含![]() 的代数式表示);
的代数式表示);
②若![]() 的面积为1,当
的面积为1,当![]() 时,
时,![]() 的最大值为-3,求
的最大值为-3,求![]() 的值.
的值.
【答案】(1)![]() ; (2)①
; (2)①![]() ;②
;②![]() 的值为0或
的值为0或![]() .
.
【解析】
(1)根据抛物线顶点的横坐标为![]() ,代入
,代入![]() 可得纵坐标,从而可求出抛物线的解析式;
可得纵坐标,从而可求出抛物线的解析式;
(2) ①设![]() ,则
,则![]() ,表示出点B,C,D的坐标, 根据点
,表示出点B,C,D的坐标, 根据点![]() 在抛物线上,把点C的坐标代入抛物线即可用a表示出t的值,再根据三角形的面积公式可求出;
在抛物线上,把点C的坐标代入抛物线即可用a表示出t的值,再根据三角形的面积公式可求出;
②根据![]() 的面积为1求出a的值,表示出抛物线的解析式,分三种情况可求出m的值.
的面积为1求出a的值,表示出抛物线的解析式,分三种情况可求出m的值.
(1)因为抛物线的顶点位于直线![]() 上,且横坐标为
上,且横坐标为![]() ,
,
所以抛物线的顶点坐标为![]() .
.
因此抛物线的解析式为![]() ;
;
(2)①如图所示.
因为![]() 轴,且
轴,且![]() ,
,
所以点![]() 的坐标为
的坐标为![]() .
.
设![]() ,则
,则![]() ,
,
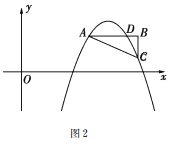
所以![]() 点的坐标为
点的坐标为![]() .
.
![]() 点的坐标为
点的坐标为![]() .
.
又点![]() 在抛物线
在抛物线![]() 上,
上,
所以![]() ,
,
整理,得![]() .
.
解得![]() (舍去),
(舍去),![]() .
.
所以![]() .
.
②若![]() 的面积为1,则
的面积为1,则![]() ,解得
,解得![]() .
.
所以抛物线的解析式为![]() .
.
分三种情况考虑:
![]() . 当
. 当![]() ,即
,即![]() 时,有
时,有![]() ,
,
整理,得![]() ,
,
此方程没有实数根;
![]() . 当
. 当![]() ,即
,即![]() 时,有
时,有![]() ,
,
解得![]() ;
;
![]() . 当
. 当![]() ,即
,即![]() 时,有
时,有![]() ,
,
整理,得![]() ,
,
解得![]() (舍去),
(舍去),![]() .
.
综上所述,![]() 的值为0或
的值为0或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
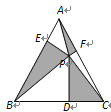
【题目】如图,等边△ABC中,P为三角形内一点,过P作PD⊥BC,PE⊥AB,PF⊥AC,连结AP、BP、CP,如果S△APF+S△BPE+S△PCD=![]() ,那么△ABC的内切圆半径为___
,那么△ABC的内切圆半径为___
查看答案和解析>>
科目:初中数学 来源: 题型:
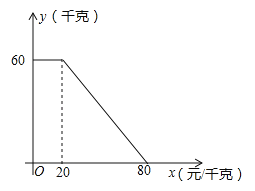
【题目】某商店以20元/千克的单价新进一批商品,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间为一次函数关系,如图所示.
(1)求y与x的函数表达式;
(2)要使销售利润达到800元,销售单价应定为每千克多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙C的半径为r,给出如下定义:若点P的横、纵坐标均为整数,且到圆心C的距离d≤r,则称P为⊙C 的关联整点.
(1)当⊙O的半径r=2时,在点D(2,-2),E(-1,0),F(0,2)中,为⊙O的关联整点的是 ;
(2)若直线![]() 上存在⊙O的关联整点,且不超过7个,求r的取值范围;
上存在⊙O的关联整点,且不超过7个,求r的取值范围;
(3)⊙C的圆心在x轴上,半径为2,若直线![]() 上存在⊙C的关联整点,求圆心C的横坐标t的取值范围.
上存在⊙C的关联整点,求圆心C的横坐标t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购,经调查:购买了3台甲型设备比购买2台乙型设备多花了16万元,购买2台甲型设备比购买3台乙型设备少花6万元.
(1)求甲、乙两种型号设备的价格;
(2)该公司经预算决定购买节省能源的新设备的资金不超过110万元,你认为该公司有几种购买方案;
(3)在(2)的条件下,已知甲型设备的产量为240吨/月,乙型设备的产量为180吨/月,若每月要求总产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中学生上网现象越来越受到社会的关注,小记者小慧随机调查了某校若干学生和家长对上网现象的看法,制作了如下的统计图①和②。请根据相关信息,解答或补全下列问题。
学生及家长对中学生上网的态度统计图 家长对中学生上网的态度统计图
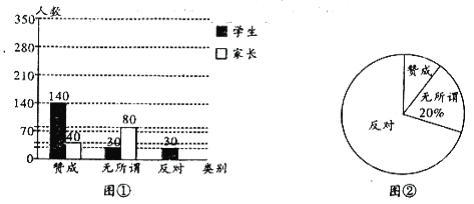
(1)补全图①;
(2)求图②中表示家长“赞成”的圆心角的度数;
(3)该校共有1600名学生,请你估计这所中学的所有学生中,对上网持“反对”态度的有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,这个图案是3世纪我国汉代数学家赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.已知AE=3,BE=2,若向正方形ABCD内随意投掷飞镖(每次均落在正方形ABCD内,且落在正方形ABCD内任何一点的机会均等),则恰好落在正方形EFGH内的概率为_____.
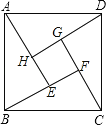
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com