
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������y=ax2+bx+c�ֱ� x����A��4��0����B��1��0������y���ڵ�C��0����3��������A��ֱ��![]() ������������һ��D��
������������һ��D��
��1���������ߵĽ���ʽ����D�����ꣻ
��2������PΪx���ϵ�һ�����㣬��Q���߶�AC�ϣ���Q�㵽x��ľ���Ϊ![]() ������PC��PQ������PCQ�ܳ���Сʱ�������P�����ꣻ
������PC��PQ������PCQ�ܳ���Сʱ�������P�����ꣻ
��3����ͼ2���ڣ�2���Ľ����£�����PD����ƽ�����Ƿ������A1P1D1��ʹ��A1P1D1�ա�APD����A1��P1��D1�Ķ�Ӧ��ֱ���A��P��D��A1P1ƽ����y�ᣬ��P1�ڵ�A1�Ϸ���������A1P1D1����������ǡ�������������ϣ������ڣ��������A1�ĺ�����m���������ڣ���˵�����ɣ�

���𰸡���1��y=![]() x2��
x2��![]() x��3����D��������2��
x��3����D����Ϊ����2��![]() ������2��PΪ��1��0������3�����ڣ�m=��
������2��PΪ��1��0������3�����ڣ�m=��![]() ��m=
��m= ![]() ��m=
��m=![]() ��m=��
��m=��![]() ��
��
��������
��1����A��B��C�����������ⷽ���鼴�ɣ�
��2�������Q���꣬����Q����x��ĶԳƵ�Q��������CQ����x���ڵ�P����ʱ��PCQ�ܳ���С�����ֱ��CQ�����ɽ�����⣮
��3��������������P1��A1����������ʱ����A1P1��y�ᣬ�ʲ����ڣ�����P1��D1����������ʱ����P1��t��![]() t2��
t2��![]() t��3����D1��
t��3����D1��![]() ��
��![]() t2��
t2��![]() t����
t����![]() ��
��![]() t2��
t2��![]() t���г����̼��ɽ��������A1��D1����������ʱ����A1����m��
t���г����̼��ɽ��������A1��D1����������ʱ����A1����m��![]() m2��
m2��![]() m��3����D1��
m��3����D1��![]() ��
��![]() m2��
m2��![]() m+3����
m+3����![]() ��
��![]() m2��
m2��![]() m+3�����г����̼��ɽ����
m+3�����г����̼��ɽ����
�⣺��1��������� ��
��
���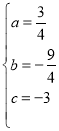 ��
��
���������߽���ʽΪy=![]() x2��
x2��![]() x��3��
x��3��
��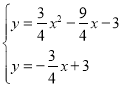 ���
���![]() ��
��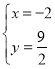 �����Ե�D����Ϊ����2��
�����Ե�D����Ϊ����2��![]() ����
����
��2����ֱ��ACΪy=![]() x��3��
x��3��![]() =
=![]() ��
��
����Q������![]() ��
��![]() ������Q����x��ĶԳƵ�Q����
������Q����x��ĶԳƵ�Q����![]() ��
��![]() ��������CQ����x���ڵ�P����ʱ��PCQ�ܳ���С��
��������CQ����x���ڵ�P����ʱ��PCQ�ܳ���С��
��ֱ��CQ��Ϊy=3x��3��
��ֱ��CQ����x��Ľ���PΪ��1��0����
��3����P1��A1����������ʱ����A1P1��y�ᣬ�ʲ����ڣ�
��P1��D1����������ʱ����P1��t��![]() t2��
t2��![]() t��3����D1��
t��3����D1��![]() ��
��![]() t2��
t2��![]() t����
t����![]() ��
��![]() t2��
t2��![]() t����
t����
��![]() t2��
t2��![]() t =
t =![]() ��
��![]() ��2��
��2��![]() ��
��![]() ����3�����t=
����3�����t=![]() ����ʱm=t=
����ʱm=t=![]() ��
��
��![]() t2��
t2��![]() t =
t =![]() ��
��![]() ��2��
��2��![]() ��
��![]() ����3�����t=
����3�����t=![]() ����ʱm=t=
����ʱm=t=![]() ��
��
��A1��D1����������ʱ����A1����m�� ![]() m2��
m2��![]() m��3����D1��
m��3����D1��![]() ��
��![]() m2��
m2��![]() m+3����
m+3����![]() ��
��![]() m2��
m2��![]() m+3����
m+3����
��![]() m2��
m2��![]() m+3=
m+3=![]() ��
��![]() ��2��
��2��![]() ��
��![]() ����3�����m=
����3�����m=![]() ��
��
��![]() m2��
m2��![]() m+3=
m+3=![]() ��
��![]() ��2��
��2��![]() ��
��![]() ����3�����m=��
����3�����m=��![]() ��
��


 ����ѧ����ϵ�д�
����ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������OABC��ֱ������ϵ�е�λ����ͼ��ʾ��A��C���������ֱ�ΪA(6��0)��C(0��3)��ֱ��![]() ��BC���ཻ�ڵ�D��
��BC���ཻ�ڵ�D��

(1)���D�����ꣻ
(2)��������![]() ����D,A���㣬��ȷ���������ߵı���ʽ��
����D,A���㣬��ȷ���������ߵı���ʽ��
(3)�裨2���������ߵĶԳ�����ֱ��OD���ڵ�M����PΪ�Գ�����һ���㣬��P��O��MΪ��������������OCD���ƣ��������������P������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
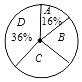
����Ŀ��Ϊ����6��6�����纣���գ�ijУ���꼶����������Ϊ����ϧ������Դ������������������ԡ���֪ʶ�������Ϊ�˽�ȫ�꼶500��ѧ���˴ξ����ɼ�������������ȡ�˲��ֲ���ѧ���ijɼ������������Ƴ����²�������ͳ�Ʊ���ͳ��ͼ����ͼ���������ͼ����Ϣ����������⣺
֪ʶ�����ɼ�����ͳ�Ʊ�
��� | ����/�� | Ƶ�� |
A | 60��x��70 | a |
B | 70��x��80 | 10 |
C | 80��x��90 | 14 |
D | 90��x��100 | 18 |
��1�����ε���һ�������ȡ���� ��������ѧ���ijɼ���
��2����1��a���� ����
��3������ȡ�IJ���ѧ���ijɼ�����λ�����ڵġ�������� ����
��4��������ƣ���У���꼶�����ɼ��ﵽ80�����ϣ���80�֣���ѧ��Լ���� ���ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ڽ�����O����B=600��CD����O��ֱ������P��CD�ӳ����ϵ�һ�㣬��AP=AC��
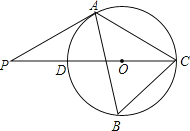
��1����֤��PA����O�����ߣ�
��2����PD=![]() ������O��ֱ����
������O��ֱ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�CA=CB����ACB=90�㣬AB=![]() ����DΪAB���е㣬�Ե�DΪԲ����Բ�Ľ�Ϊ90�������DEF����Cǡ���ڻ�EF�ϣ���ͼ����Ӱ���ֵ����Ϊ________����������У�
����DΪAB���е㣬�Ե�DΪԲ����Բ�Ľ�Ϊ90�������DEF����Cǡ���ڻ�EF�ϣ���ͼ����Ӱ���ֵ����Ϊ________����������У�
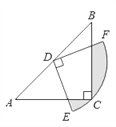
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���̶���һ����1200 m�ĵ�·�������µ�ʩ����ʽ����Ч������50%�������ǰ4���������.
��1����������̶�ԭ�ƻ�ÿ����·�����ף�
��2����������У����Ҫ�̶���ǰ2�����������ôʵ��ƽ��ÿ������·�Ĺ�Ч��ԭ�ƻ����Ӱٷ�֮����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�����Ϊ1��
��ͼ1���ֱ�AC��BC��2�ȷ֣�D1��E1����ֵ㣬����AE1��BD1���ڵ�F1���õ��ı���CD1F1E1�������S1=![]() ��
��
��ͼ2���ֱ�AC��BC��3�ȷ֣�D1��D2��E1��E2����ֵ㣬����AE2��BD2���ڵ�F2���õ��ı���CD2F2E2�������S2=![]() ��
��
��ͼ3���ֱ�AC��BC��4�ȷ֣�D1��D2��D3��E1��E2��E3����ֵ㣬����AE3��BD3���ڵ�F3���õ��ı���CD3F3E3�������S3=![]() ��
��
��
����������ɽ�����ȥ�����ֱ�AC��BC�ߣ�n+1���ȷ֣������õ��ı���CDnEnFn�������S= ��
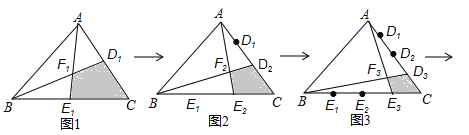
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�P��ֱ��y��2�ϵ�һ�����㣬��P�İ뾶Ϊ1��ֱ��OQ�С�P�ڵ�Q�����߶�OQȡ��Сֵʱ��Q�������Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У��Խ���BD�Ĵ�ֱƽ����MN��AD�ཻ�ڵ�M����BC�ཻ�ڵ�N������BM��DN��
(1)��֤���ı���BMDN�����Σ�
(2)��AB=4��AD=8����MD�ij���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com