
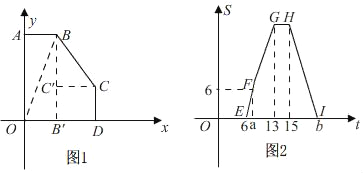
【题目】如图1,已知五边形OABCD的顶点O在坐标原点,点A在y轴上,点D在x轴上,AB∥x轴,CD∥y轴,动点P从点O出发,以每秒1单位的速度,沿五边形OABCD的边顺时针运动一周,顺次连结P,O,A三点所围成图形的面积为S,点P的运动时间为t秒,S与t之间的函数关系如图2中折线OEFGHI所示.
(1)求证:AB=2;
(2)求五边形OABCD的面积.
(3)求直线BC的函数表达式;
(4)若直线OP把五边形OABCD的面积分成1:3两部分,求点P的坐标.

【答案】(1)详见解析;(2)24;(3)y=﹣![]() x+
x+![]() ;(4)点P(
;(4)点P(![]() )或(
)或(![]() ).
).
【解析】
(1)先判断出OA=6,再利用三角形ABO的面积即可求出AB;
(2)先判断出BC,CD,进而求出B'D,再用面积的和即可得出结论;
(3)先确定出点B,C坐标,利用待定系数法即可得出结论;
(4)先判断出点P必在线段BC上,进而求出求出三角形ABM的面积,再分两种情况利用面积建立方程求解即可得出结论.
(1)连接OB,由图1,图2知,OA=6,
当点P运动到点B时,S△AOP=S△AOB=![]() ×6×AB=6,
×6×AB=6,
∴AB=2,
(2)由(1)知AB=2,
∴OA+AB=6+2=8,
∴图2中的a是8秒,
由图1,图2知,当点P从B运动到点C时,用了13﹣8=5秒钟,
∴BC=5,
点P从点C运动到点D时,△AOP的面积不变,用了15﹣13=2秒,
∴CD=2,
过点B作BB'⊥OD于B',
∴四边形OABB'是矩形,BB'=OA=6,OB'=AB=2,
过点C作CC'⊥BB'于B',
∴四边形CC'B'D是矩形,B'C'=CD=2,DB'=CC'
∴BC'=BB'﹣B'C'=4
在Rt△BC'C中,根据勾股定理得,CC'=![]() =3,
=3,
∴DB'=3,
∴OD=OB'+DB'=2+2=5,
∴S五边形OABCD的面积=S矩形AOBB'+S梯形CDB'B=2×6+![]() (2+6)×3=24;
(2+6)×3=24;
(3)由(2)知,BB'=6,OB'=2,
∴B(2,6),
由(2)知,CD=2,OD=5,
∴C(5,2),
设直线BC的解析式为y=kx+b',
∴![]() ,
,
∴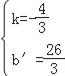 ,
,
∴直线BC的解析式为y=﹣![]() x+
x+![]() ;
;
(4)如图3,
连接OB,OC,由图2知,S△AOB=6,
由(2)知,CD=2,OD=5,
∴S△COD=5,
延长CB交y轴于M,
∴M(0,![]() ),
),
∴AM=![]() ,
,
∴S△AMB=![]() AM×AB=
AM×AB=![]()
由(2)知,S五边形OABCD的面积=24,
∴点P必在线段BC上,
设P(m,﹣![]() m+
m+![]() )(0<m<5),
)(0<m<5),
∵直线OP把五边形OABCD的面积分成1:3两部分,
∴S四边形OABP=![]() S五边形OABCD的面积=8或S四边形OABP=
S五边形OABCD的面积=8或S四边形OABP=![]() S五边形OABCD的面积=16,
S五边形OABCD的面积=16,
当S四边形OABP=8时,∴S△OPM=S四边形OABP+S△AMB=![]() =
=![]() ×
×![]() ×m,
×m,
∴m=![]() ,
,
∴P(![]() ,
,![]() )
)
当S四边形OABP'=16时,S△OP'M=S四边形OABP'+S△AMB=![]() =
=![]() ×
×![]() ×m,
×m,
∴m=![]() ,
,
∴P'(![]() ,
,![]() ),
),
即:满足题意的点P(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)试猜想BD、CE有何特殊位置关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注,某学校计划在教室内安装空气净化装置,需购进A、B两种设备,已知:购买1台A种设备和2台B种设备需要3.5万元;购买2台A种设备和1台B种设备需要2.5万元.
(1)求每台A种、B种设备各多少万元?
(2)根据学校实际,需购进A种和B种设备共30台,总费用不超过30万元,请你通过计算,求至少购买A种设备多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个正整数能表示成两个连续偶数的平方差,那么这个正整数为“神秘数”.
如:![]()
![]()
![]()
因此,4,12,20这三个数都是神秘数.
(1)28和2012这两个数是不是神秘数?为什么?
(2)设两个连续偶数为![]() 和
和![]() (其中
(其中![]() 为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
(3)两个连续奇数的平方差(取正数)是不是神秘数?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),其顶点为C,对称轴为x=1.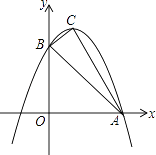
(1)求抛物线的解析式;
(2)已知点M为y轴上的一个动点,当△ABM为等腰三角形时,求点M的坐标;
(3)将△AOB沿x轴向右平移m个单位长度(0<m<3)得到另一个三角形,将所得的三角形与△ABC重叠部分的面积记为S,用m的代数式表示S.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中考体育测试前,某区教育局为了了解选报引体向上的初三男生的成绩情况,随机抽测了本区部分选报引体向上项目的初三男生的成绩,并将测试得到的成绩绘成了下面两幅不完整的统计图:
请你根据图中的信息,解答下列问题:
(![]() )写出扇形图中
)写出扇形图中![]() __________
__________![]() ,并补全条形图.
,并补全条形图.
(![]() )在这次抽测中,测试成绩的众数和中位数分别是__________个、__________个.
)在这次抽测中,测试成绩的众数和中位数分别是__________个、__________个.
(![]() )该区体育中考选报引体向上的男生共有
)该区体育中考选报引体向上的男生共有![]() 人,如果体育中考引体向上达
人,如果体育中考引体向上达![]() 个以上(含
个以上(含![]() 个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名?
个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市中小学全面开展“阳光体育”活动,某校在大课间中开设了A:体操,B:跑操,C:舞蹈,D:健美操四项活动,为了解学生最喜欢哪一项活动,随机抽取了部分学生进行调查,并将调查结果绘制成了如下两幅不完整的统计图,请根据统计图回答下列问题: 
(1)这次被调查的学生共有人.
(2)请将统计图2补充完整.
(3)统计图1中B项目对应的扇形的圆心角是度.
(4)已知该校共有学生3600人,请根据调查结果估计该校喜欢健美操的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知正比例函数![]() 与一次函数
与一次函数![]() 的
的
图像交于点A.
(1)求点A的坐标;
(2)在y轴上确定点M,使得△AOM是等腰三角形,请直接写出点M的坐标;
(3)如图,设x轴上一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交![]() 和
和![]() 的图像于点B、C,连接OC,若BC=
的图像于点B、C,连接OC,若BC=![]() OA,求△ABC的面积及点B、点C的坐标;
OA,求△ABC的面积及点B、点C的坐标;
(4)在(3)的条件下,设直线![]() 交x轴于点D,在直线BC上确定点E,使得△ADE的周长最小,请直接写出点E的坐标.
交x轴于点D,在直线BC上确定点E,使得△ADE的周长最小,请直接写出点E的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com