
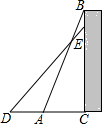
 如图,一个工人拿一个2.5米长的梯子,底端A放在距离墙根C点0.7米处,另一头B点靠墙,如果梯子的顶部下滑0.4米,梯子的底部向外滑多少米?( )
如图,一个工人拿一个2.5米长的梯子,底端A放在距离墙根C点0.7米处,另一头B点靠墙,如果梯子的顶部下滑0.4米,梯子的底部向外滑多少米?( )| A. | 0.4 | B. | 0.6 | C. | 0.7 | D. | 0.8 |
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
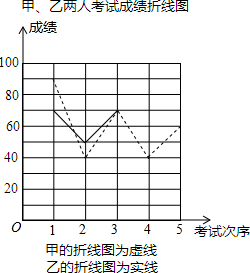 甲、乙两位同学5次数学成绩统计如表,他们的5次总成绩相同,小明根据他们的成绩绘制了尚不完整的统计图表,请同学们完成下列问题.
甲、乙两位同学5次数学成绩统计如表,他们的5次总成绩相同,小明根据他们的成绩绘制了尚不完整的统计图表,请同学们完成下列问题.| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
| 甲成绩 | 90 | 40 | 70 | 40 | 60 |
| 乙成绩 | 70 | 50 | 70 | a | 70 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
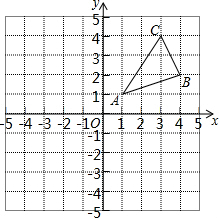 如图,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(3,4).
如图,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(3,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
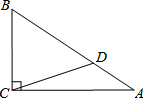 如图,Rt△ABC中,∠ACB=90°,cosA=$\frac{5}{6}$,D为AB上一点,且AD:BD=1:2,若BC=3$\sqrt{11}$,求CD的长.
如图,Rt△ABC中,∠ACB=90°,cosA=$\frac{5}{6}$,D为AB上一点,且AD:BD=1:2,若BC=3$\sqrt{11}$,求CD的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com