
 “马航失联飞机”牵动世界各国人民的心,许多国家积极组织船只进行搜救.如图,某搜救船在A处望见一可疑物P在北偏东60°方向,同时另一搜救船在B处望见可疑物P在北偏西45°方向.已知AB两处相距800海里,求B处离可疑物P的距离.(结果保留根号)
“马航失联飞机”牵动世界各国人民的心,许多国家积极组织船只进行搜救.如图,某搜救船在A处望见一可疑物P在北偏东60°方向,同时另一搜救船在B处望见可疑物P在北偏西45°方向.已知AB两处相距800海里,求B处离可疑物P的距离.(结果保留根号) 分析 作PC⊥AB于C点,设PC=x,解直角三角形APC求的AC,解直角三角形BPC求得BC和PB,然后根据题意得出关于x的方程,即方程求得x的值,即可求得PB的长.
解答 解:作PC⊥AB于C点,设PC=x,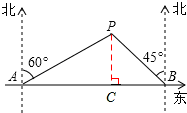
∵∠PAB=30°,∠PBA=45°.
∴BC=x,PB=$\sqrt{2}$x,AC=$\sqrt{3}$x.
∵AB=800,
∴$\sqrt{3}$x+x=800,
解得x=400($\sqrt{3}$-1),
∴PB=400($\sqrt{6}-\sqrt{2}$)(海里).
点评 本题主要考查了利用三角函数解直角三角形,把一般三角形通过作高线转化为直角三角形是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 8.01×107 | B. | 80.1×107 | C. | 8.01×108 | D. | 0.801×109 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
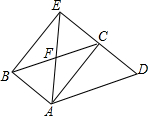 如图,在平行四边形ABCD中,AB=$\sqrt{3}$,AC=3,过点B作BE平行AC交DC的延长线于点E,连结AE,AE交BC于点F,若AB⊥AC,求△ADE的周长.
如图,在平行四边形ABCD中,AB=$\sqrt{3}$,AC=3,过点B作BE平行AC交DC的延长线于点E,连结AE,AE交BC于点F,若AB⊥AC,求△ADE的周长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com