
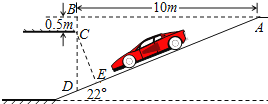
【题目】如图是某超市地下停车场入口的设计图,请根据图中数据计算CE的长度.(结果保留小数点后两位;参考数据:sin22°=0.3746,cos22°=0.9272,tan22°=0.4040)
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
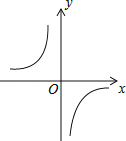
【题目】已知函数y=![]() 的图象如图,以下结论:
的图象如图,以下结论:
①m<0;
②在每个分支上y随x的增大而增大;
③若点A(﹣1,a)、点B(2,b)在图象上,则a<b;
④若点P(x,y)在图象上,则点P1(﹣x,﹣y)也在图象上.
其中正确的个数是( )
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:线段AB,BC,∠ABC=90°.求作:矩形ABCD.以下是甲、乙两同学的作业:
甲:(1)以点C为圆心,AB长为半径画弧;
(2)以点A为圆心,BC长为半径画弧;
(3)两弧在BC上方交于点D,连接AD,CD,四边形ABCD即为所求(如图1)
乙:(1)连接AC,作线段AC的垂直平分线,交AC于点M;
(2)连接BM并延长,在延长线上取一点D,使MD=MB,连接AD,CD,四边形ABCD即为所求(如图2).
对于两人的作业,下列说法正确的是( )


A. 两人都对 B. 两人都不对 C. 甲对,乙不对 D. 甲不对,乙对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=(2m+1)x+m﹣3
(1)若函数图象经过原点,求m的值;
(2)若函数的图象平行于直线y=3x﹣3,求m的值;
(3)若函数图象与y轴的交点在y轴的正半轴,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
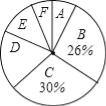
【题目】为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分
分组 | 家庭用水量x/吨 | 家庭数/户 |
A | 0≤x≤4.0 | 4 |
B | 4.0<x≤6.5 | 13 |
C | 6.5<x≤9.0 | |
D | 9.0<x≤11.5 | |
E | 11.5<x≤14.0 | 6 |
F | x>4.0 | 3 |
根据以上信息,解答下列问题
(1)家庭用水量在4.0<x≤6.5范围内的家庭有 户,在6.5<x≤9.0范围内的家庭数占被调查家庭数的百分比是 %;
(2)本次调查的家庭数为 户,家庭用水量在9.0<x≤11.5范围内的家庭数占被调查家庭数的百分比是 %;
(3)家庭用水量的中位数落在 组;
(4)若该小区共有200户家庭,请估计该月用水量不超过9.0吨的家庭数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com