
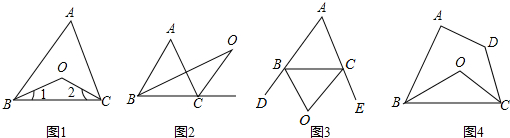
在△ABC中,P是BC边上的一个动点,以AP为直径的⊙O分别交AB、AC于点E和点F.
(1)若∠BAC=45°,EF=4,则AP的长为多少?
(2)在(1)条件下,求阴影部分面积.
(3)试探究:当点P在何处时,EF最短?请直接写出你所发现的结论,不必证明.
(1)直径AP=2OE=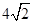 (2)S阴影=S扇形EOF-S△EOF(3)当AP⊥BC时,EF最短
(2)S阴影=S扇形EOF-S△EOF(3)当AP⊥BC时,EF最短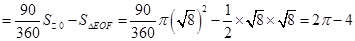
解析试题分析:解:(1)连接OE、OF,则OE=OF
∵∠EOF=2∠EAF,而∠EAF=∠BAC=45°
∴∠EOF=90°
∴△EOF是等腰直角三角形
在Rt△EOF中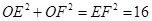
∴OE=OF=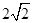
∴直径AP=2OE=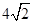 .
.
(2)S阴影=S扇形EOF-S△EOF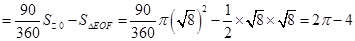 .
.
(3)在Rt△AEP中,根据垂径定理和勾股定理知,当AP取最小值时,EF的值最小;又根据点到直线的距离垂线段最短垂线段最短知当AP⊥BC时,AP最短.所以当AP⊥BC时,EF最短.
考点:圆和三角形勾股定理
点评:本题难度中等,主要考查学生对圆与三角形知识点的掌握与学习。做这类题型学生要注意培养数形结合的思维运用到考试中去。


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:阅读理解
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com