
����Ŀ����ѧ��С����ѧ�������εĽ�ƽ���ߺ���������4�����⣬��������������ͼ���ڡ�ABC�У���BAC=48�㣬��I�����ǡ�ABC����ACB��ƽ���ߵĽ��㣮
��1����գ���BIC=�������� �㣮
��2������D���������ƽ���ߵĽ��㣬��գ���BDC=�������� �㣮
��3������E���ڽǡ�ABC����ǡ�ACG��ƽ���ߵĽ��㣬��̽������BEC���BAC��������ϵ����˵�����ɣ�
��4�������⣨3���������£�����ACB������������ ��ʱ��CE��AB��
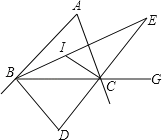
���𰸡���1��114����2��66����3����BEC![]() ��BAC�����ɼ���������4��84��
��BAC�����ɼ���������4��84��
��������
��1���ȸ��������ε��ڽǺͶ��������ABC+��ACB�Ķ����������ɸ��ݽ�ƽ���ߵ�������á�IBC+��ICB�Ķ�����Ȼ�������������ε��ڽǺͶ���������������
��2������һ���ڲ��ǵ�ƽ�����ഹֱ�ɵá�IBD=��ICD=90���������ı��ε��ڽǺͿɵá�BDC+��BIC=180�����ٽ�ϣ�1����Ľ�����ô𰸣�
��3�����ACE=��ECG=x����ABI=��IBC=y�����������ε�������ʿɵ�2x=2y+��A��x=y+��E��Ȼ��������μ��ý��ۣ�
��4������ƽ���ߵ��ж��ɵõ���ECA=��A=48��ʱCE��AB��Ȼ����ݽ�ƽ���ߵ����ʺ�ƽ�ǵĶ��弴����������
�⣺��1���ߡ�A=48����
���ABC+��ACB=180����48��=132����
�ߵ�I�����ǡ�ABC����ACB��ƽ���ߵĽ��㣬
���IBC+��ICB![]() (��ABC+��ACB)=66�������BIC=180����66��=114����
(��ABC+��ACB)=66�������BIC=180����66��=114����
�ʴ�Ϊ��114��
��2����ͼ����IBƽ�֡�ABC��DBƽ�֡�FBC��
���IBD![]() (��ABC+��FBC)= 90����
(��ABC+��FBC)= 90����
ͬ���ɵá�ICD=90����
���BDC+��BIC=180����
���BDC=180������BIC=66����
�ʴ�Ϊ��66��

��3����BEC![]() ��BAC��
��BAC��
���ɣ����ACE=��ECG=x����ABI=��IBC=y��
��2x=2y+��A�٣�x=y+��E�ڣ�
�����2���ڿɵã���E![]() ��A��
��A��
��4������ECA=��A=48��ʱ��CE��AB��
��CEƽ�֡�ACG��
���ECG=��ECA=48����
���ACB=180����48����48��=84����
�ʴ�Ϊ��84��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��ˮ������ÿǧ��2Ԫ�ļ۸�ij��ˮ������ǧ�ˣ�Ȼ����ÿǧ��4Ԫ�ļ۸���ۣ�ÿ����۳�100ǧ�ˣ�ͨ�����鷢�֣�����ˮ��ÿǧ�˵��ۼ�ÿ����1Ԫ��ÿ��ɶ��۳�200ǧ�ˣ�
��1����������ˮ��ÿǧ�˵��ۼ۽���![]() Ԫ����ÿ���������Ƕ���ǧ�ˣ�������ú�
Ԫ����ÿ���������Ƕ���ǧ�ˣ�������ú�![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
��2������ÿ��ӯ��300Ԫ���ұ�֤ÿ�������۳�260ǧ�ˣ���ôˮ�����轫ÿǧ�˵��ۼ۽��Ͷ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������֪ʶ��������A��B�����������϶�Ӧ����Ϊa��b����A��B����֮��ľ��붨��Ϊ��AB=|b-a|��
�������龳����֪��A��B��O�������ϱ�ʾ�����ֱ�Ϊ-6��10��0����M��N�ֱ��O��B������ͬʱ���������˶�����M���ٶ���ÿ��1����λ���ȣ���N���ٶ���ÿ��3����λ���ȣ����˶���ʱ��Ϊt�루t>0)��
��1����գ���OA= ��OB= ��
���ú�t��ʽ�ӱ�ʾ��AM= ��AN= ��
��2����tΪ��ֵʱ��ǡ����AN=2AM��
��3����|t-6|+|t+10|����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������jiong���ǽ�ʱ�������������һ���������Ƶ����飮��ͼ��ʾ��һ�ű߳�Ϊ20�������ε�ֽƬ����ȥ����һ����Сֱ�������κ�һ�������εõ�һ����������ͼ������Ӱ���֣������ȥ��С�����γ��Ϳ��ֱ�Ϊ![]() ��
��![]() ����ȥ������Сֱ�������ε���ֱ�DZ߳�Ҳ�ֱ�Ϊ
����ȥ������Сֱ�������ε���ֱ�DZ߳�Ҳ�ֱ�Ϊ![]() ��
��![]() ��
��
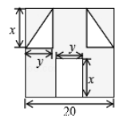
��1���ú���![]() ��
��![]() �Ĵ���ʽ��ʾ��ͼ���������������
�Ĵ���ʽ��ʾ��ͼ���������������
��2����![]() ��
��![]() ʱ�����ʱ�������������
ʱ�����ʱ�������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
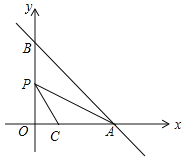
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��y=��x+m�ֱ�x�ᣬy����A��B���㣬��֪��C��2��0����
��1����ֱ��AB������Cʱ����O��ֱ��AB�ľ����� ��
��2�����PΪ�߶�OB���е㣬����PA��PC������CPA=��ABO����m��ֵ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
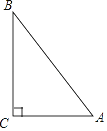
����Ŀ����ͼ���ڡ�ABC�У���C=90�㣬AB=5��BC=4����P�ڱ�AB�ϣ�����APCΪ��ACΪ���ĵ��������Σ���tan��BCP=________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ѧ���ֱ��������֪ʶ��ͬ��С����һ���⣺����ͼ��ʾ����һ�ų����ο�ƬABCD����ÿ����ȶ�Ϊ6mm�ĺ��ֽ�У�ǡ���ĸ����㶼�ں�����ϣ���֪a=36�������ο�Ƭ���ܳ����������С�������⣮����ȷ��1mm�����ο����ݣ�sin36���0.60��cos36���0.80��tan36���0.75��
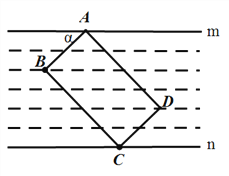
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=-x+m��y=nx+4n��n��0���Ľ���ĺ�����Ϊ-2�������н��ۣ���m��0��n��0����ֱ��y=nx+4nһ�������㣨-4��0������m��n����m=2n-2���ܵ�x��-2ʱ��nx+4n��-x+m��������ȷ���۵ĸ����ǣ�������
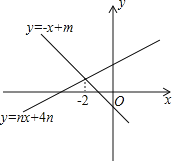
A. 1��B. 2��C. 3��D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�ǹ��Ϊ![]() �����������������������а�����Ҫ�����:
�����������������������а�����Ҫ�����:

(1)��������ƽ��ֱ������ϵ��ʹA������Ϊ(-2��4)��B������Ϊ(-4��2):
(2)�ڵڶ������ڵĸ���ϻ�һ-��C��ʹ��C���߶�AB���һ����ABΪ�ױߵĵ��������Σ���������������.���C������____��
(3) ![]() ���ܳ�=____ : ���=_ ��
���ܳ�=____ : ���=_ ��
(4)����![]() ����x��ԳƵ�
����x��ԳƵ�![]() .
.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com