
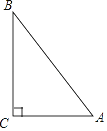
【题目】如图,在△ABC中,∠C=90°,AB=5,BC=4,点P在边AB上,若△APC为以AC为腰的等腰三角形,则tan∠BCP=________.
【答案】![]() 或
或![]()
【解析】根据勾股定理求出AC,分AC=AP和CA=CP两种情况,根据相似三角形的性质定理得到比例式,进行计算,根据正切的定义解答即可.
∵∠C=90°,AB=5,BC=4,
∴AC=![]() =3.
=3.
如图1,当AC=AP时,作PD⊥BC于D,则BP=AB-AP=2,

∵∠C=90°,PD⊥BC,
∴PD∥AC,
∴![]() ,
,
∴![]() ,
,
解得,BD=1.6,PD=1.2,
则CD=4-1.6=2.4,
tan∠BCP=![]() ;
;
如图2,当CP=CA时,作CE⊥AB于E,PD⊥BC于D,
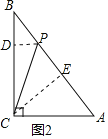
∵∠C=90°,CE⊥AB,
∴AC2=AEAB,
解得,AE=1.8,
∵CP=CA,
∴PE=AE=1.8,
则BP=1.4,
PD∥AC,
∴![]() ,
,
∴![]() ,
,
解得,BD=![]() ,PD=
,PD=![]() ,
,
则CD=4-![]() =
=![]() ,
,
tan∠BCP=![]() ,
,
故答案为:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
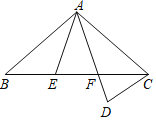
【题目】如图,△ABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.
(1)求证:△ABE≌△ACF;
(2)若∠BAE=30°,则∠ADC= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)a5·(﹣a)3﹣(﹣2a2)4;
(2)[(x﹣2y)3]3÷[(2y﹣x)2]3
(3)﹣14﹣0.510×211+(![]() )0+3÷32
)0+3÷32
(4)(![]() )﹣1+50+[2﹣(﹣3)2]
)﹣1+50+[2﹣(﹣3)2]
查看答案和解析>>
科目:初中数学 来源: 题型:
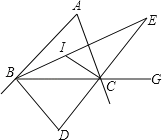
【题目】好学的小红在学完三角形的角平分线后,遇到下列4个问题,请你帮她解决.如图,在△ABC中,∠BAC=48°,点I是两角∠ABC、∠ACB的平分线的交点.
(1)填空:∠BIC= °.
(2)若点D是两条外角平分线的交点,填空:∠BDC= °.
(3)若点E是内角∠ABC、外角∠ACG的平分线的交点,试探索:∠BEC与∠BAC的数量关系,并说明理由.
(4)在问题(3)的条件下,当∠ACB等于 度时,CE∥AB?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明为了了解气温对用电量的影响,对去年自己家的每月用电量和当地气温进行了统计.去年当地每月的平均气温如图1,小明家去年月用电量如图2.
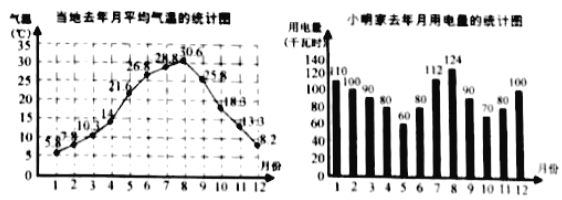
根据统计图,回答下面的问题:
(1)当地去年月平均气温的最高值、最低值各为多少?相应月份的用电量各是多少?
(2)请简单描述月用电量与气温之间的关系;
(3)假设去年小明家用电量是所在社区家庭用电量的中位数,据此他能否预测今年该社区的年用电量?请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OA1B1C1,B1A2B2C2,B2A3B3C3,···的顶点B1,B2,B3,···在x轴上,顶点C1,C2,C3···在直线y=kx+b上,若正方形OA1B1C1,B1A2B2C2的对角线OB1=2,B1B2=3, 则点C5的纵坐标是_____.
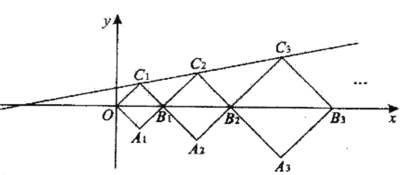
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店用不多于20000元购进甲乙两种图书共1200本进行销售.甲、乙两种图书的进价分别为每本20元、14元,甲种图书每本的售价是乙种图书每本售价的1.4倍,若用1680元在书店购买甲种图书的数量比用1400元购买乙种图书的数量少10本.
(1)甲乙两种图书的销售单价分别是多少元?
(2)书店为了让利读者,决定甲种图书售价每本降低3元,乙种图书售价每本降低2元,问书店应如何进货才能获得最大利润?最大利润是多少?(购进的两种图书全部销售完)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com