
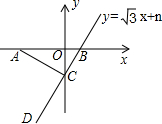
 如图,点A的坐标为(-4,0),直线y=$\sqrt{3}$x+n与坐标轴交于点B、C,连接AC,如果∠ACD=90°,则n的值为$-\frac{4\sqrt{3}}{3}$.
如图,点A的坐标为(-4,0),直线y=$\sqrt{3}$x+n与坐标轴交于点B、C,连接AC,如果∠ACD=90°,则n的值为$-\frac{4\sqrt{3}}{3}$. 分析 由直线y=$\sqrt{3}$x+n与坐标轴交于点B,C,得B点的坐标为(-$\frac{\sqrt{3}}{3}$n,0),C点的坐标为(0,n),由A点的坐标为(-4,0),∠ACD=90°,用勾股定理列出方程求出n的值.
解答 解:∵直线y=$\sqrt{3}$x+n与坐标轴交于点B,C,
∴B点的坐标为(-$\frac{\sqrt{3}}{3}$n,0),C点的坐标为(0,n),
∵A点的坐标为(-4,0),∠ACD=90°,
∴AB2=AC2+BC2,
∵AC2=AO2+OC2,BC2=OB2+OC2,
∴AB2=AO2+OC2+OB2+OC2,
即(-$\frac{\sqrt{3}}{3}$n+4)2=42+n2+(-$\frac{\sqrt{3}}{3}$n)2+n2
解得n=-$\frac{4\sqrt{3}}{3}$,n=0(舍去).
故答案为:$-\frac{4\sqrt{3}}{3}$.
点评 本题主要考查了一次函数图象上点的坐标特征及解直角三角形,解题的关键是利用勾股定理列出方程求n.


科目:初中数学 来源: 题型:解答题
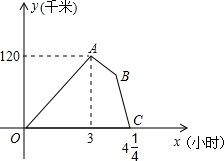 某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示.
某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 780 | B. | 800 | C. | 820 | D. | 840 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.41×106 | B. | 24.1×104 | C. | 2.41×104 | D. | 2.41×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
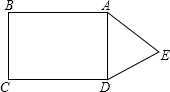 如图,这是某个小区内的道路示意图,小明家住在该小区的A处,他每天晚饭后都要从家出发随机沿着小区内的道路散步一圈后回家(每条道路不能重复走,有的道路可以不走)
如图,这是某个小区内的道路示意图,小明家住在该小区的A处,他每天晚饭后都要从家出发随机沿着小区内的道路散步一圈后回家(每条道路不能重复走,有的道路可以不走)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com