
科目:初中数学 来源: 题型:填空题
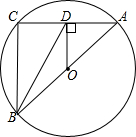 如图,AB是⊙O的直径,AC是⊙O的弦,作0D⊥AC,垂足为点D,连接BD.若AB=5cm,AC=4cm,则BD的长为$\sqrt{13}$.
如图,AB是⊙O的直径,AC是⊙O的弦,作0D⊥AC,垂足为点D,连接BD.若AB=5cm,AC=4cm,则BD的长为$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “任意一个三角形的外角和是180度”这一事件是不可能事件 | |
| B. | 一组数据1,6,3,9,8,5的中位数是6 | |
| C. | “面积相等的两个三角形全等”是必然事件 | |
| D. | 必然事件发生的概率为0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 要调查人们对“低碳生活”的了解程度,宜采用普查方式 | |
| B. | 一组数据3,4,4,6,8,5的众数和中位数都是3 | |
| C. | 必然事件的概率是100%,随机事件的概率是50% | |
| D. | 甲组数据的方差S甲2=0.13,乙组数据的方差S乙2=0.04;则乙组数据比甲组数据稳定 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
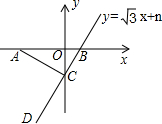 如图,点A的坐标为(-4,0),直线y=$\sqrt{3}$x+n与坐标轴交于点B、C,连接AC,如果∠ACD=90°,则n的值为$-\frac{4\sqrt{3}}{3}$.
如图,点A的坐标为(-4,0),直线y=$\sqrt{3}$x+n与坐标轴交于点B、C,连接AC,如果∠ACD=90°,则n的值为$-\frac{4\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 0.5以下 | 0.7 | 0.8 | 0.9 | 1.0 | 1.0以上 |
| 5% | 8% | 5% | 40% | 30% | 12% |
| A. | 40% | B. | 1.0 | C. | 0.9 | D. | 5% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
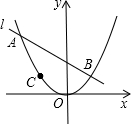 如图,已知:无论常数k为何值,直线l:y=kx+2k+2总经过定点A,若抛物线y=ax2过A,B(1,b),C(-1,c)三点.
如图,已知:无论常数k为何值,直线l:y=kx+2k+2总经过定点A,若抛物线y=ax2过A,B(1,b),C(-1,c)三点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com