
 如图,PA,PB是⊙O的两条切线,切点是A,B.如果OP=4,OA=2,那么∠AOB=( )
如图,PA,PB是⊙O的两条切线,切点是A,B.如果OP=4,OA=2,那么∠AOB=( )| A、90° | B、100° |
| C、110° | D、120° |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
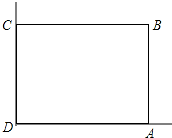 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.查看答案和解析>>
科目:初中数学 来源: 题型:
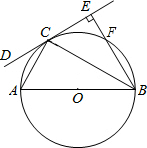 如图,AB是⊙O的直径,C为⊙O上一点,过点B作经过点C的直线CD的垂线,垂足为E (即BE⊥CD),BE交⊙O于点F,且BC平分∠ABE.
如图,AB是⊙O的直径,C为⊙O上一点,过点B作经过点C的直线CD的垂线,垂足为E (即BE⊥CD),BE交⊙O于点F,且BC平分∠ABE.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,Rt△ABC中,∠C=90°,∠A=30°,AB=4,将△ABC绕点B按顺时针方向转动一个角到△A′BC′的位置,使点A、B、C′在同一条直线上,则图中阴影部分的周长是( )
如图,Rt△ABC中,∠C=90°,∠A=30°,AB=4,将△ABC绕点B按顺时针方向转动一个角到△A′BC′的位置,使点A、B、C′在同一条直线上,则图中阴影部分的周长是( )A、4π+4
| ||
| B、4π | ||
C、2π+4
| ||
| D、2π |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com