
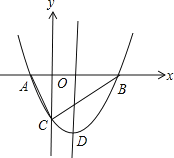
【题目】如图,抛物线![]() 与x轴交于A,B两点,与y轴交于C点,且B(3,0).
与x轴交于A,B两点,与y轴交于C点,且B(3,0).
(1)求抛物线的函数关系式;
(2)求点A和顶点D的坐标;
(3)若点M是抛物线对称轴上的一个动点,求CM+AM的最小值.
【答案】(1)![]() ;(2)A(-1,0),D(1,-4);(3)CM+AM=
;(2)A(-1,0),D(1,-4);(3)CM+AM=![]() .
.
【解析】
(1)把B的坐标代入函数的解析式,即可求得b的值,从而得到函数解析式;
(2)利用配方法即可求得顶点坐标;
(3)直线BC与抛物线的对称轴的交点就是使CM+AM取得最小值的M的点,BC的长就是最小值.
(1)∵点A(3,0)在抛物线y=x2+bx-3上,
∴b=-2,
∴抛物线解析式y=x2-2x-3,
令y=0,得x2-2x-3=0,
解得x1=3,x2=-1,
∴A坐标为(-1,0),
∵抛物线y=x2-2x-3=(x-1)2-4,
∴顶点D的坐标(1,-4);
(2)当x=0时,y=-3,
∴C(0,-3),
∴OC=3,
∵B(3,0),
∴OB=3,
由抛物线的性质可知:点A和B是对称点,
∴AM=BM,
∴AM+CM=BM+CM≥BC=3![]() .
.
∴CM+AM的最小值是3![]() .
.


科目:初中数学 来源: 题型:
【题目】随着交通道路的不断完善,带动了旅游业的发展,某市旅游景区有A、B、C、D、E等著名景点,该市旅游部门统计绘制出2017年“五一”长假期间旅游情况统计图,根据以下信息解答下列问题:
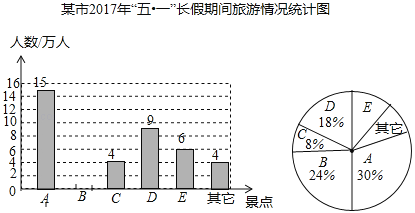
(1)2017年“五一”期间,该市周边景点共接待游客 万人,扇形统计图中A景点所对应的圆心角的度数是 ,并补全条形统计图.
(2)根据近几年到该市旅游人数增长趋势,预计2018年“五一”节将有80万游客选择该市旅游,请估计有多少万人会选择去E景点旅游?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个相似三角形的面积比为![]() ,周长和是
,周长和是![]() ,则这两个三角形的周长分别是( )
,则这两个三角形的周长分别是( )
A. 8cm和12cm B. 7cm和13cm C. 9cm和11cm D. 6cm和14cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD=BC,点E、F、G、H分别是AB、BD、CD、AC的中点,则四边形EFGH是( )
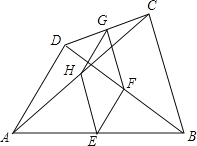
A.矩形B.菱形C.正方形D.平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂要把一批产品从![]() 地运往
地运往![]() 地,若通过铁路运输,则每千米需交运费20元,还要交装卸费400元及手续费200元,若通过公路运输,则每千米需要交运费30元,还需交手续费100元(由于本厂职工装卸,不需交装卸费).设
地,若通过铁路运输,则每千米需交运费20元,还要交装卸费400元及手续费200元,若通过公路运输,则每千米需要交运费30元,还需交手续费100元(由于本厂职工装卸,不需交装卸费).设![]() 地到
地到![]() 地的路程为
地的路程为![]() ,通过铁路运输和通过公路运输需交总运费
,通过铁路运输和通过公路运输需交总运费![]() 元和
元和![]() 元.
元.
(1)求![]() 和
和![]() 关于
关于![]() 的函数表达式.
的函数表达式.
(2)若![]() 地到
地到![]() 地的路程为
地的路程为![]() ,哪种运输可以节省总运费?
,哪种运输可以节省总运费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市2017年国内生产总值(GDP)比2016年增长了12%,由于受到国际金融危机的影响,预计2018比2017年增长7%,若这两年GDP年平均增长率为![]() %,则
%,则![]() %满足的关系是( )
%满足的关系是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
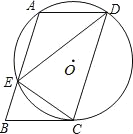
【题目】如图,在ABCD中,过A、C、D三点的⊙O交AB于点E,连接DE、CE,∠CDE=∠BCE.
(1)求证:AD=CE;
(2)判断直线BC与⊙O的位置关系,并说明理由;
(3)若BC=4,DE=10,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com