
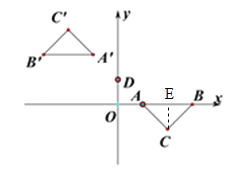
【题目】如图,在平面直角坐标系中,点A,B,D的坐标为(1,0),(3,0),(0,1),点C在第四象限,∠ACB=90°,AC=BC.若△ABC与△A'B'C'关于点D成中心对称,则点C'的坐标为______.

【答案】(-2,3)
【解析】分析:过C作CE⊥AB于E,由A、B的坐标,可得AB的长,由等腰三角形的性质得到BE,AE,CE的长,从而得到点C的坐标,再根据待定系数法,可得直线DA的函数解析式,根据中点坐标公式,可得答案.
详解:过C作CE⊥AB于E.
∵∠ACB=90°,AC=BC,∴E为AB的中点,∴CE=![]() AB.
AB.
∵A(1,0),B(3,0),∴E(2,0),AB=2,CE=AE=BE=1,∴C(2,-1).
设DA的解析式为y=kx+b,将A,D点坐标代入,得:
![]() ,解得
,解得![]() ,AD的解析式为y=﹣x+1.
,AD的解析式为y=﹣x+1.
设C′的坐标为(x,y),则D为CC′的中点.由中点坐标公式,得:
x+2=0,y-1=2,解得:x=-2,y=3.∴C′(-2,3).故答案为:(﹣2,3).


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】数轴是一个非常重要的数学工具,它使数和数轴上的点建立对应关系,解释了数与点之间的内在联系,它是“数形结合”的基础。
如图,数轴上有三个点A、B、C,它们可以沿着数轴左右移动,请回答
![]() )
)
(1)将点B向右移动4个单位长度后到达点D,点D表示的数是 ,A、D两点之间的距离是 ;
(2)移动点A到达E点,使B、C、E三点的其中某一点到其它两点的距离相等,写出点E在数轴上对应的数值 ;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一空旷场地上设计一落地为矩形ABCD的小屋,AB+BC=10m.拴住小狗的10m长的绳子一端固定在B点处,小狗在不能进入小屋内的条件下活动,其可以活动的区域面积为S(m2).
①如图1,若BC=4m,则S=m.
②如图2,现考虑在(1)中的矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域,使之变成落地为五边形ABCED的小屋,其它条件不变.则在BC的变化过程中,当S取得最小值时,边BC的长为m.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,借助直角三角板可以找到一元二次方程的实数根,比如对于方程 ![]() ,操作步骤是:
,操作步骤是:
第一步:根据方程系数特征,确定一对固定点A(0,1),B(5,2);
第二步:在坐标平面中移动一个直角三角板,使一条直角边恒过点A,另一条直角边恒过点B;
第三步:在移动过程中,当三角板的直角顶点落在x轴上点C处时,点C 的横坐标m即为该方程的一个实数根(如图1)
第四步:调整三角板直角顶点的位置,当它落在x轴上另一点D处时,点D 的横坐标为n即为该方程的另一个实数根。
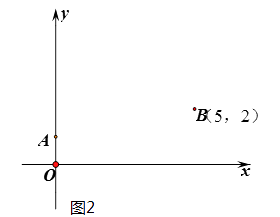
(1)在图2 中,按照“第四步“的操作方法作出点D(请保留作出点D时直角三角板两条直角边的痕迹)
(2)结合图1,请证明“第三步”操作得到的m就是方程 ![]() 的一个实数根;
的一个实数根;
(3)上述操作的关键是确定两个固定点的位置,若要以此方法找到一元二次方程 ![]() 的实数根,请你直接写出一对固定点的坐标;
的实数根,请你直接写出一对固定点的坐标;
(4)实际上,(3)中的固定点有无数对,一般地,当 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 与a,b,c之间满足怎样的关系时,点P(
与a,b,c之间满足怎样的关系时,点P( ![]() ,
, ![]() ),Q(
),Q( ![]() ,
, ![]() )就是符合要求的一对固定点?
)就是符合要求的一对固定点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)﹣(﹣7)﹣(﹣5)+(﹣4)
(2)(﹣3![]() )+12.5+(﹣16
)+12.5+(﹣16![]() )﹣(﹣2.5)
)﹣(﹣2.5)
(3)(﹣24)×(![]() )
)
(4)18×(﹣![]() )+13×
)+13×![]() ﹣4×
﹣4×![]()
(5)﹣12018 - ![]() ×[2×(﹣2)+10].
×[2×(﹣2)+10].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,BC=3,点E,F,G,H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为( )
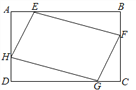
A. 7 B. 10 C. 14 D. 15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以AB为直径的⊙O经过AC的中点D,DE⊥BC于点E. 
(1)求证:DE是⊙O的切线;
(2)当AB=4 ![]() ,∠C=30°时,求图中阴影部分的面积(结果保留根号和π).
,∠C=30°时,求图中阴影部分的面积(结果保留根号和π).
查看答案和解析>>
科目:初中数学 来源: 题型:
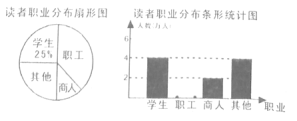
【题目】学习成为现代人的时尚,我,市有关部门统计了最近6个月到图书馆的读者和职业分布情况,并做了下列两个不完整的统计图.请你根据图中提供的信息,解答下列问题:
(l)求在统汁的这段时问内,到图书馆阅读的总人次:
(2)请补全条形统汁图,并求扇形统计图中表示“商人”的扇形的圆心角度数;
(3)符5月份到图书馆的读者共20000人次,估汁其中约有多少人次读者是职工?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,系列结论:(1)4a+b=0;(2)4a+c>2b;(3)5a+3c>0;(4)若点A(﹣2,y1),点B( ![]() ,y2),点C(
,y2),点C( ![]() ,y2)在该函数图象上,则y1<y3<y2;(5)若m≠2,则m(am+b)>2(2a+b),其中正确的结论有( )
,y2)在该函数图象上,则y1<y3<y2;(5)若m≠2,则m(am+b)>2(2a+b),其中正确的结论有( ) 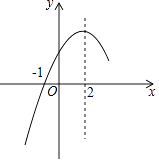
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com