
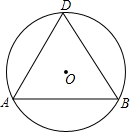
 如图,已知⊙O的半径为2,弦AB的长为2$\sqrt{3}$,D是优弧$\widehat{ADB}$上的任意一点(点D不与A,B重合).
如图,已知⊙O的半径为2,弦AB的长为2$\sqrt{3}$,D是优弧$\widehat{ADB}$上的任意一点(点D不与A,B重合).分析 (1)作OC⊥AB于C,根据垂径定理得AC=BC=$\frac{1}{2}$AB=$\sqrt{3}$,在Rt△AOC中利用锐角三角函数可求出∠OAC=30°,则根据三角形内角和定理得到∠AOB=120°.
(2)设D点到AB的距离为h,由三角形面积公式可知,三角形面积S是h的一次函数,当h最大时,S最大,求得h的最大值,代入即可求得.
解答 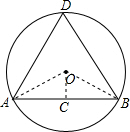 解:(1)作OC⊥AB于C,则AC=BC=$\frac{1}{2}$AB=$\sqrt{3}$,
解:(1)作OC⊥AB于C,则AC=BC=$\frac{1}{2}$AB=$\sqrt{3}$,
在Rt△AOC中,∵OA=2,AC=$\sqrt{3}$,
∴cos∠OAC=$\frac{AC}{OA}$=$\frac{\sqrt{3}}{2}$,
∴∠OAC=30°,
∴∠AOB=180°-2∠OAB=120°;
(2)∵∠OAC=30°,
∴OC=$\frac{1}{2}$OA=1,
设D点到AB的距离为h,
∴S△ABD=$\frac{1}{2}$AB•h=$\sqrt{3}$h,
∴当h最大时,S最大,
∵当D、O、C在一条直线上时,h最大,
∴h=OD+OC=2+1=3,
∴S的最大值为3$\sqrt{3}$.
点评 此题考查了圆周角定理、垂径定理以及三角函数等知识.注意准确作出辅助线是解此题的关键.


 作业辅导系列答案
作业辅导系列答案科目:初中数学 来源: 题型:选择题
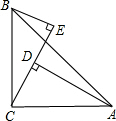 如图所示,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D,BE=7cm,AD=15cm,则DE的长是( )
如图所示,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D,BE=7cm,AD=15cm,则DE的长是( )| A. | 7 | B. | 8 | C. | 15 | D. | 22 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 ,那么加上卡片上的数字;如果抽到的卡片形如
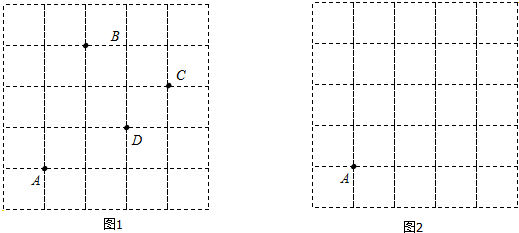
,那么加上卡片上的数字;如果抽到的卡片形如 ,那么减去卡片上的数字;②比较两人所抽4张卡片的计算结果,结果大的为胜者.小明抽到如图①所示的4张卡片,小丽抽到如图②所示的4张卡片,请你通过计算(要求有具体的计算过程),指出本次游戏的获胜者.
,那么减去卡片上的数字;②比较两人所抽4张卡片的计算结果,结果大的为胜者.小明抽到如图①所示的4张卡片,小丽抽到如图②所示的4张卡片,请你通过计算(要求有具体的计算过程),指出本次游戏的获胜者.
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y2<y3 | D. | y2<y1<y3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,点D在△ABC外部,点E在BC边上,DE交AC于F,若∠1=∠2,∠D=∠C,AE=AB,则( )
如图所示,点D在△ABC外部,点E在BC边上,DE交AC于F,若∠1=∠2,∠D=∠C,AE=AB,则( )| A. | △ABC≌△AFE | B. | △AFE≌△ADC | C. | △AFE≌△DFC | D. | △ABC≌△AED |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com