
【题目】如图,在边长为![]() 的正方形
的正方形![]() 中,点
中,点![]() 是边
是边![]() 中点,点
中点,点![]() 在边
在边![]() 上,且
上,且![]() ,设
,设![]() 与
与![]() 交于点
交于点![]() ,则
,则![]() 的面积是________.
的面积是________.

【答案】![]()
【解析】
过点G作GM⊥AD于M,如图,先证明△ABE∽△DEF,利用相似三角形的性质计算出DF=![]() ,再利用正方形的性质判断△DGM为等腰直角三角形得到DM=MG,设DM=x,则MG=x,EM=1-x,然后证明△EMG∽△EDF,再利用相似三角形的性质计算出GM,再利用三角形面积公式计算S△DEG即可.
,再利用正方形的性质判断△DGM为等腰直角三角形得到DM=MG,设DM=x,则MG=x,EM=1-x,然后证明△EMG∽△EDF,再利用相似三角形的性质计算出GM,再利用三角形面积公式计算S△DEG即可.
过点G作GM⊥AD于M,如图,

∵FE⊥BE,
∴∠AEB+∠DEF=90°,
而∠AEB+∠ABE=90°,
∴∠ABE=∠DEF,
而∠A=∠EDF,
∴△ABE∽△DEF,
∴AB:DE=AE:DF,即2:1=1:DF,
∴DF=![]() ,
,
∵四边形ABCD为正方形,
∴∠ADB=45°,
∴△DGM为等腰直角三角形,
∴DM=MG,
设DM=x,则MG=x,EM=1-x,
∵MG∥DF,
∴△EMG∽△EDF,
∴MG:DF=EM:ED,即x:![]() =(1-x):1,解得x=
=(1-x):1,解得x=![]() ,
,
∴DM= MG=![]() ,
,
∴S△DEG=![]() ED·MG=
ED·MG=![]() ×1×
×1×![]() =
=![]() .
.
故答案为:![]() .
.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】如图,延长平行四边形![]() 的边
的边![]() 到
到![]() ,使
,使![]() ,连结
,连结![]() 交
交![]() 于点
于点![]() .
.
![]() 试说明:
试说明:![]() ;
;
![]() 连结
连结![]() ,
,![]() 相交于
相交于![]() ,连结
,连结![]() ,问
,问![]() 与
与![]() 有怎样的数量关系与位置关系,说明理由;
有怎样的数量关系与位置关系,说明理由;
![]() 若
若![]() ,连接
,连接![]() ,四边形
,四边形![]() 是什么特殊四边形,说明理由;
是什么特殊四边形,说明理由;
![]() 在
在![]() 的条件下,当
的条件下,当![]() 满足________条件时,四边形
满足________条件时,四边形![]() 是正方形.
是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() 、
、![]() 为对角线,点
为对角线,点![]() 、
、![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 、
、![]() 边的中点,下列说法:
边的中点,下列说法:
①当![]() 时,
时,![]() 、
、![]() 、
、![]() 、
、![]() 四点共圆.
四点共圆.
②当![]() 时,
时,![]() 、
、![]() 、
、![]() 、
、![]() 四点共圆.
四点共圆.
③当![]() 且
且![]() 时,
时,![]() 、
、![]() 、
、![]() 、
、![]() 四点共圆.
四点共圆.
其中正确的是( )

A. ①② B. ①③ C. ②③ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,将两个全等的三角板如图摆放,其中△ABC和ΔADE的直角顶点重合在点A处,∠ADE=∠ABC=60°,且点D在AC上,点B在AE上,∠C=∠E=30°,AB=AD,AC=AE,BC=DE,BC和DE相交于点F.求证:CF=EF.

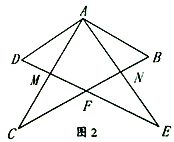
(2)如图2,将这两个三角板如图摆放,直角顶点A仍然重合,BC与DE相交于点F,AC与DE交于点M,AE和BC交于点N.猜想CF和EF还相等吗?说明理由.
(3)如图3,在(2)的基础上,若∠DAM=30°.求证:线段DF和AC互相垂直平分.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市“青山绿水”行动中,某社区计划对面积为![]() 的区域进行绿化,经投标由甲、乙两个工程队来完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,如果两队各自独立完成面积为
的区域进行绿化,经投标由甲、乙两个工程队来完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,如果两队各自独立完成面积为![]() 区域的绿化时,甲队比乙队少用6天.
区域的绿化时,甲队比乙队少用6天.
(1)求甲、乙两工程队每天各能完成多少面积的绿化;
(2)若甲队每天绿化费用是1.2万元,乙队每天绿化费用为0.5万元,社区要使这次绿化的总费用不超过40万元,则至少应安排乙工程队绿化多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AD是△ABC的角平分线,E、F分别是边AB、AC的中点,连接DE、DF,在不再连接其他线段的前提下,要使四边形AEDF成为菱形,还需添加一个条件,这个条件可以是 ;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com