
【题目】如图,一次函数y1=ax+b的图象与反比例 函数y2= ![]() 的图象交于M,N两点.
的图象交于M,N两点. 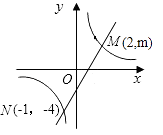
(1)利用图中条件,求反比例函数和一次函数的解析式;
(2)观察图象,比较y1与y2的大小.
【答案】
(1)解:∵反比例函数y2= ![]() 的图象过点N(﹣1,﹣4),
的图象过点N(﹣1,﹣4),
∴k=﹣1×(﹣4)=4,
∴反比例函数的解析式为y2= ![]() .
.
∵点M(2,m)在反比例函数y2= ![]() 的图象上,
的图象上,
∴m= ![]() =2,
=2,
∴点M的坐标为(2,2).
将M(2,2)、N(﹣1,﹣4)代入y1=ax+b中,
![]() ,解得:
,解得: ![]() ,
,
∴一次函数的解析式为y=2x﹣2
(2)解:观察函数图象,由两函数图象的上下位置关系可知:
当x<﹣1或0<x<2时,y1<y2;当x=﹣1或x=2时,y1=y2;当﹣1<x<0或x>2时,y1>y2
【解析】(1)根据点N的坐标利用反比例函数图象上点的坐标特征即可求出反比例函数解析式,由点M的横坐标结合反比例函数图象上点的坐标特征即可得出点M的坐标,再根据点M、N的坐标利用待定系数法即可求出一次函数解析式,此题得解;(2)观察图形,根据两函数图象的上下位置关系即可得出结论.


科目:初中数学 来源: 题型:
【题目】如图,直线L1:y=bx+c与抛物线L2:y=ax2的两个交点坐标分别为A(m,4),B(1,1). 
(1)求m的值;
(2)过动点P(n,0)且垂直于x轴的直线与L1 , L2的交点分别为C,D,当点C位于点D上方时,请直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店打出促销广告:最潮新款服装30件,每件售价300元.若一次性购买不超过10件时,售价不变;若一次性购买超过10件时,每多买1件,所买的每件服装的售价均降低3元.已知该服装成本是每件200元,设顾客一次性购买服装x件时,该网店从中获利y元.
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)顾客一次性购买多少件时,该网店从中获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,其图象的一部分如图所示则①abc<0;②a﹣b+c<0;③3a+c<0;④当﹣1<x<3时,y>0.其中判断正确的有( )个. 
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,平移抛物线y=x2﹣2x+3,使平移后的抛物线经过点A(﹣2,0),且与y轴交于点B,同时满足以A,O,B为顶点的三角形是等腰直角三角形,求平移后的抛物线的解析式. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=15,AC=12,BC=9,经过点C且与边AB相切的动圆与CB、CA分别相交于点E、F,则线段EF长度的最小值是( ) 
A.![]()
B.![]()
C.![]()
D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com