
【题目】解下列方程:
(1)2x2﹣x=1
(2)x2+4x+2=0.
【答案】
(1)
解:2x2﹣x﹣1=0,
(2x+1)(x﹣1)=0,
2x+1=0或x﹣1=0,
所以x1=﹣ ![]() ,x2=1
,x2=1
(2)
解:△=42﹣4×2=8,
x= ![]() =﹣2±
=﹣2± ![]() ,
,
所以x1=﹣2+ ![]() ,x2=﹣2﹣
,x2=﹣2﹣ ![]()
【解析】(1)先把方程化为一般式,然后利用因式分解法解方程;(2)利用求根公式法解方程.
【考点精析】认真审题,首先需要了解配方法(左未右已先分离,二系化“1”是其次.一系折半再平方,两边同加没问题.左边分解右合并,直接开方去解题),还要掌握公式法(要用公式解方程,首先化成一般式.调整系数随其后,使其成为最简比.确定参数abc,计算方程判别式.判别式值与零比,有无实根便得知.有实根可套公式,没有实根要告之)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=ax+b的图象与反比例 函数y2= ![]() 的图象交于M,N两点.
的图象交于M,N两点. 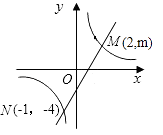
(1)利用图中条件,求反比例函数和一次函数的解析式;
(2)观察图象,比较y1与y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的顶点A在第一象限,AB∥x轴,AD∥y轴,且对角线的交点与原点O重合.在边AB从小于AD到大于AD的变化过程中,若矩形ABCD的周长始终保持不变,则经过动点A的反比例函数y= ![]() (k≠0)中k的值的变化情况是( )
(k≠0)中k的值的变化情况是( ) 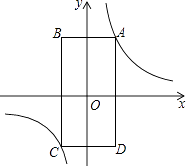
A.一直增大
B.一直减小
C.先增大后减小
D.先减小后增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC、EC分别为四边形ABCD和EFCG的对角线,点E在△ABC内,∠CAE+∠CBE=90°,当四边形ABCD和EFCG均为正方形时,连接BF. 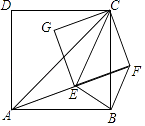
(1)求证:△CAE∽△CBF;
(2)若BE=1,AE=2,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD,FE分别交AC,BC于点D,E两点,当∠DFE在△ABC内绕顶点F旋转时(点D不与A,C重合),给出以下个结论:①CD=BE ②四边形CDFE不可能是正方形 ③△DFE是等腰直角三角形 ④S四边形CDFE= ![]() S△ABC , 上述结论中始终正确的有( )
S△ABC , 上述结论中始终正确的有( ) 
A.①②③
B.②③④
C.①③④
D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程:x2﹣2(m+1)x+m2+5=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若原方程的两个实数根为x1、x2 , 且满足x12+x22=|x1|+|x2|+2x1x2 , 求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC= ![]() OB.
OB. 
(1)求证:AB是⊙O的切线;
(2)若∠ACD=45°,OC=2,求弦CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com