
【题目】已知,如图,![]() ,
,![]() ,求证:
,求证:![]() .
.

证明:∵![]() ,
,
∴________________(同旁内角互补,两直线平行),
∴![]() =________(两直线平行,内错角相等),
=________(两直线平行,内错角相等),
又∵![]() (已知),
(已知),
∴________________(内错角相等,两直线平行),
∴![]() =________(两直线平行,内错角相等),
=________(两直线平行,内错角相等),
∴![]() -
-![]() =________________,
=________________,
即![]() .
.
 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:
【题目】按图填空,并注明理由.
⑴完成正确的证明:如图,已知AB∥CD,求证:∠BED=∠B+∠D
证明:过E点作EF∥AB(经过直线外一点有且只有一条直线与这条直线平行)
∴∠1= ( )
∵AB∥CD(已知)
∴EF∥CD(如果两条直线与同一直线平行,那么它们也平行)
∴∠2= ( )
又∠BED=∠1+∠2
∴∠BED=∠B+∠D (等量代换).
⑵如图,在△ABC中,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
解:因为EF∥AD(已知)
所以∠2=∠3.( )
又因为∠1=∠2,所以∠1=∠3.(等量代换)
所以AB∥ ( )
所以∠BAC+ =180°( ).
又因为∠BAC=70°,所以∠AGD=110°.


图⑴ 图⑵
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值:
(1)(9x3y-12xy3+3xy2)÷(-3xy)-(2y+x)(2y-x),其中x=1,y=-2;
(2)(m-n)(m+n)+(m+n)2-2m2,其中m、n满足方程组![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,以任意两点P(x1,y1)、Q(x2,y2)为端点的线段的中点坐标为![]() .
.
(1)如图(1),C为线段AB中点,A点坐标为(0,4),B点坐标为(5,4),则点C的坐标为
(2)如图(2),F为线段DE中点,D点坐标为(﹣4,﹣3),E点坐标为(1,﹣3).则点F的坐标为________
应用:
(1)如图(3),长方形ONDF的对角线相交于点M,ON,OF分别在x轴和y轴上,O为坐标原点,点D的坐标为(4,3),则点M的坐标为 ;
(2)在直角坐标系中,有A(﹣1,2),B(3,1),C(1,4)三点,另有一点D与A,B,C构成平行四边形的顶点,直接写出D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE、DF恰好分别经过点B、C.△ABC中,∠A=50°,求∠DBA+∠DCA的度数.
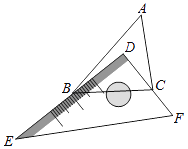
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB∥CD,

求:(1)在图(1)中∠B+∠D=?(2)在图(2)中∠B+∠E1+∠D=?(3)在图(3)中∠B+∠E1+∠E2+…+∠En﹣1+∠En+∠D=?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3,已知A(1,5) 、A1(2,5) 、A2(4,5) 、A3(8,5) 、B(2,0) 、B1(4,0) 、B2(8,0) 、B3(16,0):若按此规律,将△OAB进行n次变换,得到△OAnBn。推测An的坐标是___________,Bn的坐标是___________。( )

A. (2n,5)(2n+1,0) B. (2n-1,5)(2n+1,0) C. (2n,5)(2n,0) D. (2n+1,5)(2n+1,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com