
 如图,已知在直角梯形ABCD中,AD∥BC,AB=BC,E为AB中点,BD⊥CE,BD,CE相交于M,连接AM交BC于G点.
如图,已知在直角梯形ABCD中,AD∥BC,AB=BC,E为AB中点,BD⊥CE,BD,CE相交于M,连接AM交BC于G点.| AM |
| MG |
| 5 |
2
| ||
| 5 |
3
| ||
| 5 |
| AD |
| GB |
| 3 |
| 2 |
| 2x |
| 3 |
| 4 |
| 3 |
| S△ADM |
| S△GBM |
| 9 |
| 4 |
| 4 |
| 9 |
| 8 |
| 9 |
|
| DA2+AB2 |
| 5 |
| BM |
| BA |
| BE |
| BD |

| BM |
| 2x |
| x | ||
|
2
| ||
| 5 |
| 5 |
2
| ||
| 5 |
3
| ||
| 5 |
| DM |
| BM |
| 3 |
| 2 |
| AM |
| MG |
| AD |
| GB |
| DM |
| BM |
| 3 |
| 2 |
| AD |
| GB |
| 3 |
| 2 |
| 2x |
| 3 |
| 2x |
| 3 |
| 4 |
| 3 |
| S△ADM |
| S△GBM |
| DM |
| BM |
| 9 |
| 4 |
| 4 |
| 9 |
| 8 |
| 9 |


 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
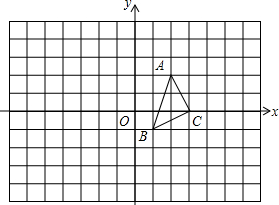 已知平面直角坐标系中,△ABC的三个顶点的坐标分别为A(2,2),B(1,-1),C(3,0).
已知平面直角坐标系中,△ABC的三个顶点的坐标分别为A(2,2),B(1,-1),C(3,0).查看答案和解析>>
科目:初中数学 来源: 题型:
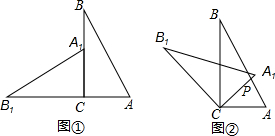 将两块含30°角且大小相同的直角三角板如图①摆放,将图①中△A1B1C绕点C顺时针旋转45°得到图②,点P是A1C与AB的交点,若AP=2,AC的长为
将两块含30°角且大小相同的直角三角板如图①摆放,将图①中△A1B1C绕点C顺时针旋转45°得到图②,点P是A1C与AB的交点,若AP=2,AC的长为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com