
【题目】【问题探究】
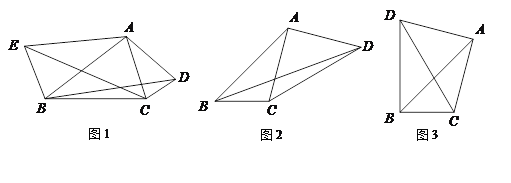
(1)如图1,锐角△ABC中,分别以AB、AC为边向外作等腰△ABE和等腰△ACD,使AE=AB,AD=AC,∠BAE=∠CAD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由.
【深入探究】
(2)如图2,四边形ABCD中,AB=7cm,BC=3cm,∠ABC=∠ACD=∠ADC=45,求BD的长.
(3)如图3,在(2)的条件下,当△ACD在线段AC的左侧时,求BD的长.
【答案】(1)BD=CE.理由参见解析;(2)![]() cm;(3)(
cm;(3)(![]() )cm.
)cm.
【解析】试题分析:(1)首先根据等式的性质证明∠EAC=∠BAD,则根据SAS即可证明△EAC≌△BAD,根据全等三角形的性质即可证明;
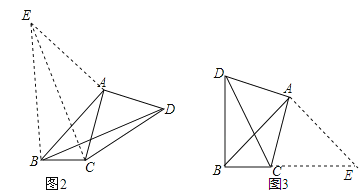
(2)在△ABC的外部,以A为直角顶点作等腰直角△BAE,使∠BAE=90°,AE=AB,连接EA、EB、EC,证明△EAC≌△BAD,证明BD=CE,然后在直角三角形BCE中利用勾股定理即可求解;
(3)在线段AC的右侧过点A作AE⊥AB于点A,交BC的延长线于点E,证明△EAC≌△BAD,证明BD=CE,即可求解.
试题解析:解:(1)BD=CE.
理由是:∵∠BAE=∠CAD,∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD,在△EAC和△BAD中,∵AE=AB,∠EAC=∠BAD,AC=AD,∴△EAC≌△BAD,∴BD=CE;
(2)如图2,在△ABC的外部,以A为直角顶点作等腰直角△BAE,使∠BAE=90°,AE=AB,连接EA、EB、EC.∵∠ACD=∠ADC=45°,∴AC=AD,∠CAD=90°,∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD,在△EAC和△BAD中,∵AE=AB,∠EAC=∠BAD,AC=AD,∴△EAC≌△BAD,∴BD=CE.∵AE=AB=3,∴BE=![]() =
=![]() (不化简不必扣分),∠AEC=∠AEB=45°,又∵∠ABC=45°,∴∠ABC+∠ABE=45°+45°=90°,∴EC=
(不化简不必扣分),∠AEC=∠AEB=45°,又∵∠ABC=45°,∴∠ABC+∠ABE=45°+45°=90°,∴EC=![]() =
=![]() =
=![]() ,∴BD=CE=
,∴BD=CE=![]() ;
;
(3)如图3,在线段AC的右侧过点A作AE⊥AB于点A,交BC的延长线于点E,连接BE.∵AE⊥AB,∴∠BAE=90°,又∵∠ABC=45°,∴∠E=∠ABC=45°,∴AE=AB=3,BE=![]() =
=![]() ,又∵∠ACD=∠ADC=45°,∴∠BAE=∠DAC=90°,∴∠BAE﹣∠BAC=∠DAC﹣∠BAC,即∠EAC=∠BAD,在△EAC和△BAD中,∵AE=AB,∠EAC=∠BAD,AC=AD,∴△EAC≌△BAD,∴BD=CE,∵BC=1,∴BD=CE=
,又∵∠ACD=∠ADC=45°,∴∠BAE=∠DAC=90°,∴∠BAE﹣∠BAC=∠DAC﹣∠BAC,即∠EAC=∠BAD,在△EAC和△BAD中,∵AE=AB,∠EAC=∠BAD,AC=AD,∴△EAC≌△BAD,∴BD=CE,∵BC=1,∴BD=CE=![]() =
=![]() (cm).
(cm).


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
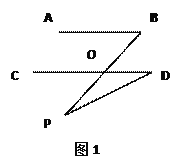
【题目】平面内的两条直线有相交和平行两种位置关系.
(1)AB∥CD.如图1,点P在AB,CD外部时,由AB∥CD,有∠B=∠BOD.又因为∠BOD是△POD的外角,故∠BOD=∠BPD +∠D ,得∠BPD=∠B-∠D.如图2,将点P移到AB,CD内部,以上结论是否成立?若不成立,则∠BPD,∠B,∠D之间有何数量关系?请证明你的结论.
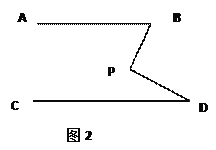
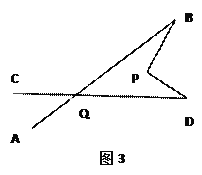
(2)在图2中,将直线AB绕点B按逆时针方向旋转一定角度交直线CD于点Q,如图3,则∠BPD,∠B,∠D,∠BQD之间有何数量关系?说明理由.
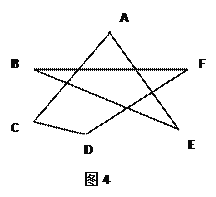
(3)根据(2)的结论,求图4中∠A+∠B+∠C+∠D+∠E+∠F的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果将抛物线y=x2+2向右平移1个单位,那么所得新抛物线的表达式是( )
A.y=x2+3
B.y=(x﹣1)2+2
C.y=(x+1)2+2
D.y=x2+1
查看答案和解析>>
科目:初中数学 来源: 题型:
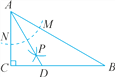
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧,分别交AB,AC于点M和N,再分别以点M,N为圆心,大于![]() MN长为半径画弧,两弧交于点P,连结AP并延长,交BC于点D,则下列说法中,正确的个数是( )
MN长为半径画弧,两弧交于点P,连结AP并延长,交BC于点D,则下列说法中,正确的个数是( )
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC∶S△ABC=1∶3.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.
(1)求证:△ADC≌△ECD;
(2)当点D在什么位置时,四边形ADCE是矩形,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
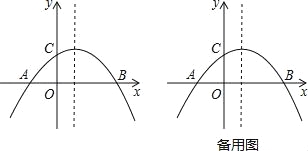
【题目】如图,已知抛物线y=ax2+bx+c与x轴相交于A(﹣2,0),B(4,0),与y轴相交于点C,且抛物线经过点(2,2).
(1)求此抛物线的解析式;
(2)在抛物线的对称轴上找一点H,使AH+CH最小,并求出点H的坐标;
(3)在第四象限内,抛物线上是否存在点M,是的以点A、B、M为顶点的三角形与△ABC相似?若存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com