
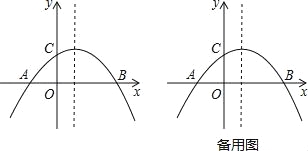
【题目】如图,已知抛物线y=ax2+bx+c与x轴相交于A(﹣2,0),B(4,0),与y轴相交于点C,且抛物线经过点(2,2).
(1)求此抛物线的解析式;
(2)在抛物线的对称轴上找一点H,使AH+CH最小,并求出点H的坐标;
(3)在第四象限内,抛物线上是否存在点M,是的以点A、B、M为顶点的三角形与△ABC相似?若存在,请求出点M的坐标;若不存在,请说明理由.
【答案】(1)抛物线解析式为y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)H(1,![]() );
);
(3)不存在,理由见解析.
【解析】
试题分析:(1)把A(﹣2,0),B(4,0),(2,2)代入抛物线解析式列方程组解决问题.
(2)如图1,连接BC交对称轴于点H,由对称轴的性质和两点之间线段最短的性质可得:此时AH+CH=BH+CH=BC最小,利用待定系数法求出直线BC解析式,与抛物线对称轴联立求出H坐标即可;
(3)在第四象限内,抛物线上存在点M,使得以点A、B、M为顶点的三角形与△ACB相似,分两种情况考虑:(i)当△ACB∽△ABM时;(ii)当△ACB∽△MBA时,利用相似三角形的判定与性质,确定出m的值即可.
试题解析:(1)A(﹣2,0),B(4,0),(2,2)代入抛物线解析式
得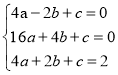 解得
解得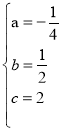 ,∴抛物线解析式为y=﹣
,∴抛物线解析式为y=﹣![]() x2+
x2+![]() x+2.
x+2.
(2)如图1,连接BC交对称轴于点H,
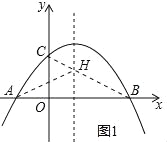
由对称轴的性质和两点之间线段最短的性质可得:此时AH+CH=BH+CH=BC最小,
设直线BC的解析式为y=kx+b,把B与C坐标代入得:
![]() ,解得:
,解得: ,∴直线BC解析式为y=﹣
,∴直线BC解析式为y=﹣![]() x+2,
x+2,
令x=1,得到y=![]() ,即H(1,
,即H(1,![]() );
);
(3)不存在.
分两种情况考虑:(i)不妨设△ACB∽△ABM时,如图2中,

则有∠CAB=∠MAB=45°,∴直线AM为y=﹣x﹣2,由 解得
解得![]() 或
或![]() ,
,
∴点M坐标(8,﹣10),此时AM=10![]() ,∵
,∵![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,∴
,∴![]() ,
,
∴△ABC与△AMB不相似.
(ii)不妨设△ACB∽△MBA时,如图3中,

则∠ABC=∠MAB,∴BC∥AM,∵直线BC解析式为y=﹣![]() x+2,∴直线AM解析式为y=﹣
x+2,∴直线AM解析式为y=﹣![]() x﹣1,
x﹣1,
由 解得
解得![]() 或
或![]() ,∴AM=4
,∴AM=4![]() ,∵
,∵![]() =
=![]() =
=![]() ,
, ![]() ,∴
,∴![]()
,△ACB与△MBA不相似.
综上所述,在第四象限内,抛物线上不存在点M,使得以点A、B、M为顶点的三角形与△ACB相似.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】【问题探究】
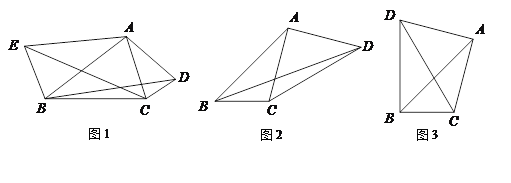
(1)如图1,锐角△ABC中,分别以AB、AC为边向外作等腰△ABE和等腰△ACD,使AE=AB,AD=AC,∠BAE=∠CAD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由.
【深入探究】
(2)如图2,四边形ABCD中,AB=7cm,BC=3cm,∠ABC=∠ACD=∠ADC=45,求BD的长.
(3)如图3,在(2)的条件下,当△ACD在线段AC的左侧时,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.减去一个数等于加上这个数
B.两个相反数相减得0
C.两个数相减,差一定小于被减数
D.两个数相减,差不一定小于被减数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中不能使两个直角三角形全等的是( )
A. 两条直角边对应相等 B. 两个锐角对应相等
C. 一条直角边和斜边对应相等 D. 一个锐角和斜边对应相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次蜡烛实验中,甲、乙两根蜡烛燃烧时剩余部分的高度![]() (cm)与燃烧时间
(cm)与燃烧时间![]() (h)的关系如图所示. 请根据图像所提供的信息解答下列各问题:
(h)的关系如图所示. 请根据图像所提供的信息解答下列各问题:

(1)甲乙两根蜡烛燃烧前的高度分别是 ,从点燃到燃尽所用的时间分别是 ;
(2)分别求出甲、乙两根蜡烛燃烧时![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)当![]() 为何值时,甲、乙两根蜡烛在燃烧的过程中的高度相等?
为何值时,甲、乙两根蜡烛在燃烧的过程中的高度相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BE,CF分别是△ABC中AC,AB边上的高线,在BE的延长线上取点P,使PB=AC,在CF的延长线上取点Q,使CQ=AB.求证:AQ⊥AP.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在昆明市轨道交通的修建中,规划在A、B两地修建一段地铁,点B在点A的正东方向,由于A、B之间建筑物较多,无法直接测量,现测得古树C在点A的北偏东45°方向上,在点B的北偏西60°方向上,BC=400m,请你求出这段地铁AB的长度.(结果精确到1m,参考数据:![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解题: 阅读:解不等式(x+1)(x﹣3)>0
解:根据两数相乘,同号得正,原不等式可以转化为: ![]() 或
或 ![]()
解不等式组 ![]() 得:x>3
得:x>3
解不等式组 ![]() 得:x<﹣1
得:x<﹣1
所以原不等式的解集为:x>3或x<﹣1
问题解决:根据以上阅读材料,解不等式(x﹣2)(x+3)<0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com