
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E. 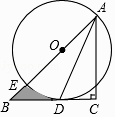
(1)求证:AD平分∠BAC;
(2)若CD=1,求图中阴影部分的面积(结果保留π).
【答案】
(1)证明:连接DE,OD.
∵BC相切⊙O于点D,
∴∠CDA=∠AED,
∵AE为直径,
∴∠ADE=90°,
∵AC⊥BC,
∴∠ACD=90°,
∴∠DAO=∠CAD,
∴AD平分∠BAC;
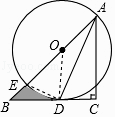
(2)∵在Rt△ABC中,∠C=90°,AC=BC,
∴∠B=∠BAC=45°,
∵BC相切⊙O于点D,
∴∠ODB=90°,
∴OD=BD,∴∠BOD=45°,
设BD=x,则OD=OA=x,OB= ![]() x,
x,
∴BC=AC=x+1,
∵AC2+BC2=AB2,
∴2(x+1)2=( ![]() x+x)2,
x+x)2,
∴x= ![]() ,
,
∴BD=OD= ![]() ,
,
∴图中阴影部分的面积=S△BOD﹣S扇形DOE= ![]() ﹣
﹣ ![]() =1﹣
=1﹣ ![]()
【解析】(1)连接DE,OD.利用弦切角定理,直径所对的圆周角是直角,等角的余角相等证明∠DAO=∠CAD,进而得出结论;(2)根据等腰三角形的性质得到∠B=∠BAC=45°,由BC相切⊙O于点D,得到∠ODB=90°,求得OD=BD,∠BOD=45°,设BD=x,则OD=OA=x,OB= ![]() x,根据勾股定理得到BD=OD=
x,根据勾股定理得到BD=OD= ![]() ,于是得到结论.
,于是得到结论.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】请先观察下列算式,再填空:32-12=8×1,52-32=8×2,72-52=8×3;92-72=8×4,…,通过观察归纳,写出用n(n为正整数)反映这种规律的一般结论:_______________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正六边形A1B1C1D1E1F1的边长为1,它的六条对角线又围成一个正六边形A2B2C2D2E2F2 , 如此继续下去,则正六边形A4B4C4D4E4F4的面积是. 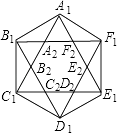
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=55°,求:
(1)∠FED的度数;
(2)∠FEG的度数;
(3)∠1和∠2的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形OABC的三个顶点A、B、C在以O为圆心的半圆上,过点C作CD⊥AB,分别交AB、AO的延长线于点D、E,AE交半圆O于点F,连接CF. 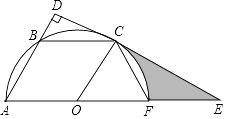
(1)判断直线DE与半圆O的位置关系,并说明理由;
(2)①求证:CF=OC; ②若半圆O的半径为12,求阴影部分的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com