
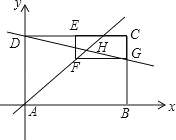
【题目】如图,在矩形ABCD中,点A为坐标原点,点B在x轴正半轴,点D在y轴正半轴,点C坐标为(6,m),点E是CD的中点,以CE为一边在矩形ABCD的内部作矩形CEFG,使点F在直线y=x上,交线段BC于点G,直线DG的函数表达式为y=-![]() x+4,直线DG和AF交于点H.
x+4,直线DG和AF交于点H.
(1)求m的值;
(2)求点H的坐标;
(3)判断直线BE是否经过点H,并说明理由.
【答案】(1)4(2)(![]() ,
,![]() )(3)直线BE过点H
)(3)直线BE过点H
【解析】
试题分析:(1)根据矩形性质和直线DG的与y轴的交点,确定出点C,B,D的坐标,即可;
(2)由两条直线的解析式联立即可求出点H的坐标;
(3)确定出直线BE的解析式,再判断点H是否在该直线上.
试题解析:(1)∵直线DG的函数表达式为y=﹣![]() x+4,
x+4,
∴D(0,4),
∵四边形ABCD是矩形,且C(6,m),
∴m=4,
∴C(6,4)
(2)∵直线AF:y=x与直线DG:y=﹣![]() x+4的交点为H,
x+4的交点为H,
∴ ,
,
∴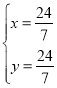 ,
,
∴H(![]() ,
,![]() )
)
(3)直线BE过点H,
理由:
∵直线DG解析式为y=﹣![]() x+4,直线BC解析式为x=6,
x+4,直线BC解析式为x=6,
∴G(6,3),
∴点F的纵坐标为3,
∵点F在直线AF上,
∴F点的横坐标为3,
∴F(3,3),
∴点E的横坐标为3,
∵直线DC解析式为y=4,
∴E(3,4),
∵B(6,0),
∴直线BE解析式为y=﹣![]() x+8,
x+8,
当x=![]() 时,y=﹣
时,y=﹣![]() ×
×![]() +8=
+8=![]() ,
,
∴直线BE过点H.


科目:初中数学 来源: 题型:
【题目】下列式子可以用“=”连接的是( )
A.5+4_______12-5
B.7+(-4)______7-(+4)
C.2+4(-2)______-12
D.2(3-4)_____23-4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校在经典诵读活动中,对全校学生用A,B,C,D四个等级进行评价,现从中随机抽取若干个学生进行调查,绘制出了两幅不完整的统计图,如图所示,请你根据图中信息解答下列问题: 
(1)共抽取了多少个学生进行调查?
(2)分别求出B等级的人数和图乙中B等级所占圆心角的度数.
(3)将图甲中的折线统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
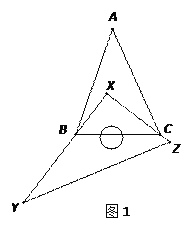
【题目】(1)如图1,有一块直角三角板XYZ(其中∠X=90°)放置在△ABC上,恰好三角板XYZ的两条直角边XY,XZ分别经过B,C两点,且直角顶点X在△ABC内部.
①若∠A=40°,∠ABC+∠ACB= °;∠XBC+∠XCB= °;
②试判断∠A与∠XBA+∠XCA之间存在怎样数量关系?并写出证明过程.
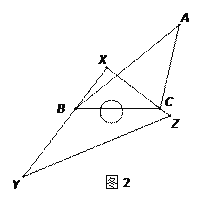
(2)如图2,如果直角顶点X在△ABC外部,试判断∠A、∠XBA、∠XCA之间又存在怎样的数量关系?(只写出答案,无需证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD的边长为8,⊙O经过点C和点D,且与AB相切于点E.
(1)求⊙O的半径;
(2)如图2,平移⊙O,使点O落在BD上,⊙O经过点D,BC与⊙O交于M,N,求MN2的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般情况下 ![]() 不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得
不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得 ![]() 成立的一对数a,b为“相伴数对”,记为(a,b).
成立的一对数a,b为“相伴数对”,记为(a,b).
(1)若(1,b)是“相伴数对”,求b的值;
(2)写出一个“相伴数对”(a,b),其中a≠0,且a≠1;
(3)若(m,n)是“相伴数对”,求代数式m﹣ ![]() ﹣[4m﹣2(3n﹣1)]的值.
﹣[4m﹣2(3n﹣1)]的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com