
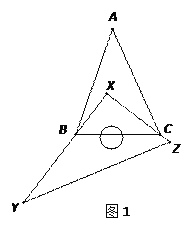
【题目】(1)如图1,有一块直角三角板XYZ(其中∠X=90°)放置在△ABC上,恰好三角板XYZ的两条直角边XY,XZ分别经过B,C两点,且直角顶点X在△ABC内部.
①若∠A=40°,∠ABC+∠ACB= °;∠XBC+∠XCB= °;
②试判断∠A与∠XBA+∠XCA之间存在怎样数量关系?并写出证明过程.
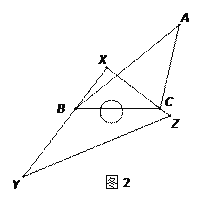
(2)如图2,如果直角顶点X在△ABC外部,试判断∠A、∠XBA、∠XCA之间又存在怎样的数量关系?(只写出答案,无需证明).
【答案】(1)①140,90;②∠A+∠XBA+∠XCA=90°,证明见解析;(2)∠A+(∠XBA-∠XCA)=90°
【解析】试题分析:(1)①根据三角形内角和定理可得∠ABC+∠ACB=180°﹣∠A=140°,∠XBC+∠XCB=180°﹣∠XBC=90°,进而可求出∠ABX+∠ACX的度数;
②根据三角形内角和定义有90°+(∠ABX+∠ACX)+∠A=180°,则可得出结论.
(2)由②的解题思路可得:∠A+(∠XBA-∠XCA)=90°.
(1)①若∠A=40°,∠ABC+∠ACB= 140 °;
∠XBC+∠XCB= 90 °;
②∠A+∠XBA+∠XCA=90°(或等式的变形也可以)
证明:∵∠X=90°
∴∠XBC+∠XCB=180°-∠X=90°
∵∠A+∠ABC+∠ACB=180°,
∴∠A+(∠XBA+∠XCA)+(∠XBC+∠XCB)=180°,
∴∠A+(∠XBA+∠XCA)=180°-90°=90°,
∴∠A=90°-(∠XBA+∠XCA)
(2) ∠A+(∠XBA-∠XCA) =90°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】若a+b=2,则称a与b是关于1的平衡数.
(1)3与 是关于1的平衡数,5﹣![]() 与 是关于1的平衡数;
与 是关于1的平衡数;
(2)若(m+![]() )×(1﹣
)×(1﹣![]() )=﹣5+3
)=﹣5+3![]() ,判断m+
,判断m+![]() 与5﹣
与5﹣![]() 是否是关于1的平衡数,并说明理由.
是否是关于1的平衡数,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
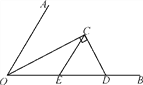
【题目】(10分)如图,∠AOB=60°,OC平分∠AOB,C为角平分线上一点,过点C作CD⊥OC,垂足为C,交OB于点D,CE∥OA交OB于点E.判断△CED的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生利用双休时间去距学校10km的炎帝故里参观,一部分学生骑自行车先走,过了20min后,其余学生乘汽车沿相同路线出发,结果他们同时到达。已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度和汽车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
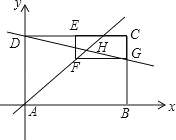
【题目】如图,在矩形ABCD中,点A为坐标原点,点B在x轴正半轴,点D在y轴正半轴,点C坐标为(6,m),点E是CD的中点,以CE为一边在矩形ABCD的内部作矩形CEFG,使点F在直线y=x上,交线段BC于点G,直线DG的函数表达式为y=-![]() x+4,直线DG和AF交于点H.
x+4,直线DG和AF交于点H.
(1)求m的值;
(2)求点H的坐标;
(3)判断直线BE是否经过点H,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列判断:①在数轴上,原点两旁的两个点所表示的数都是互为相反数;②任何正数必定大于它的倒数;③5ab, ![]() ,
, ![]() 都是整式;④x2﹣xy+y2是按字母y的升幂排列的多项式,其中判断正确的是( )
都是整式;④x2﹣xy+y2是按字母y的升幂排列的多项式,其中判断正确的是( )
A.①②
B.②③
C.③④
D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校实行学案式教学,需印制若干份数学学案,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示:
(1)填空:甲种收费的函数关系式是 ;乙种收费的函数关系式是 ;
(2)该校某年级每次需印制100~450(含100和450)份学案,选择哪种印刷方式较合算?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )

A. ∠BCA=∠F; B. ∠B=∠E; C. BC∥EF ; D. ∠A=∠EDF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com