
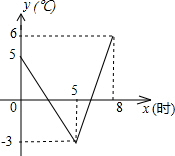 ��������������֣��������¼����½���0�����µ����������Ϊ��˪������ij��ֲ����������0�����µ�ʱ�䳬��3Сʱ��������˪���ֺ������ȡԤ����ʩ����ͼ������̨ij�췢���ĸõ���������Ϣ��Ԥ���˴���0ʱ��8ʱ������ʱ��仯���������0ʱ��5ʱ��5ʱ��8ʱ��ͼ��ֱ�����һ�κ�����ϵ������ͼ����Ϣ��
��������������֣��������¼����½���0�����µ����������Ϊ��˪������ij��ֲ����������0�����µ�ʱ�䳬��3Сʱ��������˪���ֺ������ȡԤ����ʩ����ͼ������̨ij�췢���ĸõ���������Ϣ��Ԥ���˴���0ʱ��8ʱ������ʱ��仯���������0ʱ��5ʱ��5ʱ��8ʱ��ͼ��ֱ�����һ�κ�����ϵ������ͼ����Ϣ������ ��1������ͼ�ֱ�Ӻ���ͼ����ȡ���㣬���ô���ϵ������������������Ľ���ʽ��
��2��y1��y2�ֱ����0����������������ʽ�������x1��x2����ͼ���п�֪��x2-x1����ֲ������0�����µ�ʱ�䣬��3���ȽϾͿ����ˣ�
��� �⣺��1����0ʱ��5ʱ�ĺ�������ʽΪy=k1x+b1��
�ߵ㣨0��5������5��-3������ͼ���ϣ�
��$\left\{\begin{array}{l}{b=5}\\{5k+b=-3}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-\frac{8}{5}}\\{b=5}\end{array}\right.$��
��0ʱ��5ʱ�ĺ�������ʽΪy=-$\frac{8}{5}$x+5��
��5ʱ��8ʱ�ĺ�������ʽΪy=k2x+b2��
�ߵ㣨5��-3������8��6������ͼ���ϣ�
��$\left\{\begin{array}{l}{-3=5k+b}\\{6=8k+b}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=3}\\{b=-18}\end{array}\right.$��
��5ʱ��8ʱ�ĺ�������ʽΪy=3x-18��
��2����y=0����x1=$\frac{25}{8}$��x2=6��
��x2-x1=$\frac{23}{8}$��3��
���Ҫ��ȡ��˪����ʩ��
���� ���⿼������һ�κ������ʵ�����⣬����ϵ������������ʽ���Լ���ͬһ������������֮��ľ����֪ʶ���������մ���ϵ������������ʽ�ǽ���Ĺؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
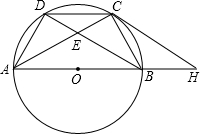 ��ͼ����A��B��C��D��ֱ��ΪAB�ġ�O���ĸ��㣬C���ӻ�$\widehat{BD}$���е㣬AC��BD�ڵ�E��AE=2��EC=1��
��ͼ����A��B��C��D��ֱ��ΪAB�ġ�O���ĸ��㣬C���ӻ�$\widehat{BD}$���е㣬AC��BD�ڵ�E��AE=2��EC=1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
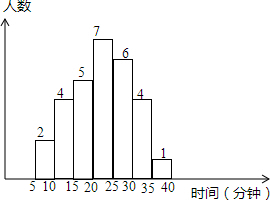 һ��ѧϰС���ij��˫�����ڼҲμӼ����Ͷ����õĴ���ʱ�䣨�������ƣ����˳������飬���ͼ����Ϣ�������С������ȡ������������29��
һ��ѧϰС���ij��˫�����ڼҲμӼ����Ͷ����õĴ���ʱ�䣨�������ƣ����˳������飬���ͼ����Ϣ�������С������ȡ������������29���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3x��x+y��+3x2+3xy | B�� | -2x2-2xy=-2x��x+y�� | C�� | ��x+5����x-5��=x2-25 | D�� | x2+x+1=x��x+1��+1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
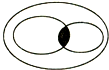 ��֪ʶ�ṹ������ƽ���ı��Ρ����Ρ����Ρ������εİ�����ϵ������ͼ��ʾ��������������Բ��ʾ����ƽ���ı��Σ���Ӱ���ֱ�ʾ���������Σ�
��֪ʶ�ṹ������ƽ���ı��Ρ����Ρ����Ρ������εİ�����ϵ������ͼ��ʾ��������������Բ��ʾ����ƽ���ı��Σ���Ӱ���ֱ�ʾ���������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3+5-x=2��x-4�� | B�� | 3-5-x=2��4-x�� | C�� | 3-5-x=2��x-4�� | D�� | 3-5+x=-2��x-4�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com