
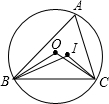
 如图所示,已知△ABC的内心为I,外心为O.
如图所示,已知△ABC的内心为I,外心为O. 所对的圆周角,由圆周角定理得∠A=
所对的圆周角,由圆周角定理得∠A= ∠BOC.
∠BOC. ∠ABC,∠ICB=
∠ABC,∠ICB= ∠ACB.
∠ACB. ∠ABC+
∠ABC+ ∠ACB)
∠ACB) (180°-∠A)=90°+
(180°-∠A)=90°+ ∠A.
∠A. ∠A=90°+
∠A=90°+ ×
× ∠BOC=90°+
∠BOC=90°+ ∠BOC,
∠BOC, ∠BOC.
∠BOC. ∠A;当I是内心时,则∠BIC=90°+
∠A;当I是内心时,则∠BIC=90°+ ∠A.
∠A. 

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com