
【题目】已知在平面直角坐标系中有三点![]() 、
、![]() 、
、![]() ,请回答如下问题:
,请回答如下问题:
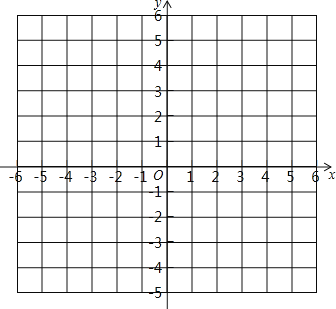
(1)在坐标系内描出点![]() 的位置:
的位置:
(2)求出以![]() 三点为顶点的三角形的面积;
三点为顶点的三角形的面积;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使以
,使以![]() 三点为顶点的三角形的面积为10,若存在,请直接写出点
三点为顶点的三角形的面积为10,若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
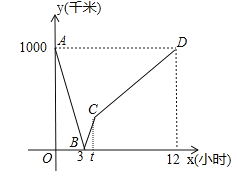
【题目】首条贯通丝绸之路经济带的高铁线﹣宝兰客专进入全线拉通试验阶段,宝兰客专的通车对加快西北地区与“一带一路”沿线国家和地区的经贸合作、人文交流具有十分重要的意义.试运行期间,一列动车从西安开往西宁,一列普通列车从西宁开往西安,两车同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系,根据图象进行一下探究:
【信息读取】
(1)西宁到西安两地相距 千米,两车出发后 小时相遇;
(2)普通列车到达终点共需 小时,普通列车的速度是 千米/小时.
【解决问题】
(3)求动车的速度;
(4)普通列车行驶t小时后,动车到达终点西宁,求此时普通列车还需行驶多少千米到达西安?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我国民间流传着许多诗歌形式的数学算题,这些题目叙述生动、活泼,它们大都是关于方程和方程组的应用题.由于诗歌的语言通俗易懂、雅俗共赏,因而一扫纯数学的枯燥无味之感,令人耳目一新,回味无穷.请根据下列诗意列方程组解应用题.
周瑜寿属:而立之年督东吴,早逝英年两位数;十比个位正小三,个位六倍与寿符;哪位同学算得快,多少年寿属周瑜?诗的意思是:周瑜病逝时的年龄是一个大于30的两位数,其十位上的数字比个位数字小3,个位上的数字的6倍正好等于这个两位数,求这个两位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人共同计算一道整式乘法题:(2x+a)(3x+b).甲由于把第一个多项式中的“+a”看成了“﹣a”,得到的结果为6x2+11x﹣10;乙由于漏抄了第二个多项式中x的系数,得到的结果为2x2﹣9x+10.
(1)求a、b的值.
(2)计算这道乘法题的正确结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于点F.
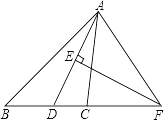
(1)求证:∠FAD=∠FDA;
(2)若∠B=50°,求∠CAF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,F是CD上一点,E是BF上一点,连接AE、AC、DE.若AB=AC,AD=AE,∠BAC=∠DAE=70°,AE平分∠BAC,则下列结论中:①△ABE≌△ACD:②BE=EF;③∠BFD=110°;④AC垂直平分DE,正确的个数有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题再现:
数形结合是解决数学问题的一种重要的思想方法,借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性,从而可以帮助我们快速解题.初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释.
例如:利用图形的几何意义证明完全平方公式.
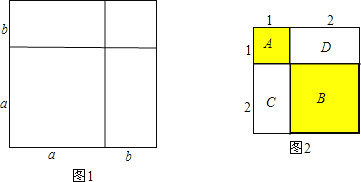
证明:将一个边长为a的正方形的边长增加b,形成两个矩形和两个正方形,如图1:
这个图形的面积可以表示成:
(a+b)2或 a2+2ab+b2
∴(a+b)2 =a2+2ab+b2
这就验证了两数和的完全平方公式.
类比解决:
(1)请你类比上述方法,利用图形的几何意义证明平方差公式.(要求画出图形并写出推理过程)
问题提出:如何利用图形几何意义的方法证明:13+23=32?
如图2,A表示1个1×1的正方形,即:1×1×1=13
B表示1个2×2的正方形,C与D恰好可以拼成1个2×2的正方形,因此:B、C、D就可以表示2个2×2的正方形,即:2×2×2=23而A、B、C、D恰好可以拼成一个(1+2)×(1+2)的大正方形.
由此可得:13+23=(1+2)2=32
尝试解决:
(2)请你类比上述推导过程,利用图形的几何意义确定:13+23+33= .(要求写出结论并构造图形写出推证过程).
(3)问题拓广:
请用上面的表示几何图形面积的方法探究:13+23+33+…+n3= .(直接写出结论即可,不必写出解题过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com