
【题目】如图,⊙![]() 是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙
是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙![]() 于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF。
于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF。
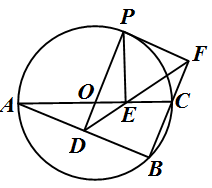
(1)若∠POC=60°,AC=12,求劣弧PC的长;(结果保留π)
(2)求证:OD=OE;
(3)求证:PF是⊙![]() 的切线。
的切线。
【答案】(1)2π;(2)证明过程见解析;(3)证明过程见解析.
【解析】
试题分析:(1)根据直径得出半径的长度,然后根据弧长的计算公式进行求解;(2)、根据垂直得出∠ADO=∠PEO,对顶角相等,半径相等得出△ADO和△PEO全等,从而得出OD=OE;(3)连接PC,根据直径得出∠ABC=90°,从而说明PD∥BC,根据已知条件结合(2)得出△PCE和△PFC全等,从而说明∠OPF=90°,得出切线.
试题解析:(1)由直径AC=12得半径OC=6
劣弧PC的长为![]()
(2)∵ OD⊥AB,PE⊥AC
∴ ∠ADO=∠PEO=90°
在△ADO和△PEO中,∠ADO=∠PEO,∠AOD=∠POE,OA=OP
∴ △ADO≌△PEO
∴ OD=OE
(3)连接PC,由AC是直径知BC⊥AB,又OD⊥AB,
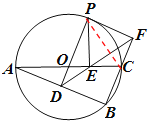
∴ PD∥BF
∴ ∠OPC=∠PCF,∠ODE=∠CFE
由(2)知OD=OE,则∠ODE=∠OED,又∠OED=∠FEC
∴ ∠FEC=∠CFE
∴ EC=FC
由OP=OC知∠OPC=∠OCE
∴ ∠PCE =∠PCF
在△PCE和△PFC中,EC=FC
∠PCE=∠PCF PC=PC
∴ △PCE≌△PFC
∴ ∠PFC =∠PEC=90°
由∠PDB=∠B=90°可知∠OPF=90°即OP⊥PF
∴ PF是⊙![]() 的切线
的切线


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案科目:初中数学 来源: 题型:
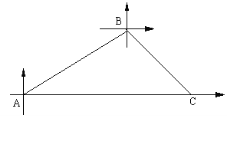
【题目】甲、乙两条轮船同时从港口A出发,甲轮船以每小时30海里的速度沿着北偏东60°的方向航行,乙轮船以每小时15海里的速度沿着正东方向行进,1小时后,甲船接到命令要与乙船会和,于是甲船改变了行进的速度,沿着东南方向航行,结果在小岛C处与乙船相遇.假设乙船的速度和航向保持不变,求港口A与小岛C之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 的三个顶点坐标分别为A(2,-4),B(3,-2), C(6,-3)
的三个顶点坐标分别为A(2,-4),B(3,-2), C(6,-3)
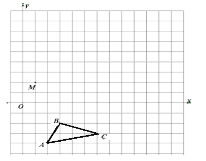
(1)画出△ABC关于![]() 轴对称的△A1B1C1;
轴对称的△A1B1C1;
(2)以M点为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2 ,使△A2B2C2与△A1B1C1的相似比为2:1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,直线x=﹣1是对称轴,有下列判断:①b﹣2a=0;②4a﹣2b+c<0;③a﹣b+c=﹣9a;④若(﹣3,y1),(![]() ,y2)是抛物线上两点,则y1>y2,其中正确的个数是( )
,y2)是抛物线上两点,则y1>y2,其中正确的个数是( )
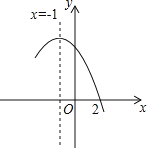
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
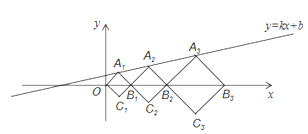
【题目】在平面直角坐标系xOy中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2,…,按图所示的方式放置.点A1、A2、A3,…和点B1、B2、B3,…分别在直线y=kx+b和x轴上.已知C1(1,-1),C2(![]() ,
,![]() ),则点A3的坐标是__________.
),则点A3的坐标是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com