
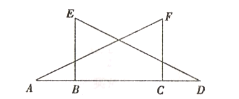
【题目】如图,△ACF≌△DBE,其中点A、B、C、D在一条直线上.
(1)若BE⊥AD,∠F=62°,求∠A的大小.
(2)若AD=9cm,BC=5cm,求AB的长.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E是边BC的中点,DE的延长线与AB的延长线相交于点F.
(1)求证:△CDE≌△BFE;
(2)试连接BD、CF,判断四边形CDBF的形状,并证明你的结论

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲,乙两人以相同路线前往距离单位10![]() 的培训中心参加学习.图中
的培训中心参加学习.图中![]() 分别表示甲,乙两人前往目的地所走的路程s
分别表示甲,乙两人前往目的地所走的路程s![]() 随时间(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8
随时间(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8![]() 后遇到甲;④乙出发6分钟后追上甲.其中正确的有( )
后遇到甲;④乙出发6分钟后追上甲.其中正确的有( )
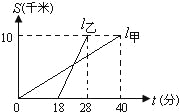
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有3600名学生,为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
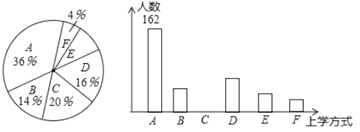
(1)参与本次问卷调查的学生共有 人,其中选择D类的人数有 人;
(2)在扇形统计图中,求E类对应的扇形圆心角![]() 的度数,并补全C对应的条形统计图;
的度数,并补全C对应的条形统计图;
(3)若将A、B、C.D.E这四类上学方式视为“绿色出行”,请估计该校选择“绿色出行”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
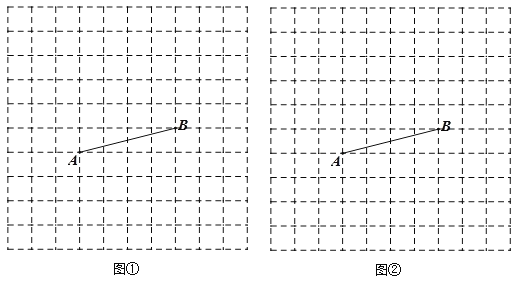
【题目】如图,方格纸中每个小正方形的边长都是1个单位长度.线段AB的端点A、B都在格点上,请你仅用无刻度的直尺完成下列作图.(保留必要的作图痕迹,不必写作法)
(1)在图①中以AB为边作一个正方形ABCD;
(2)在图②中以点A、点B为顶点作一个面积为12的菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明骑自行车上学,开始以正常速度匀速行驶,但行至中途时,自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,他比修车前加快了速度继续匀速行驶,下面是行驶路程s(m)关于时间t(min)的函数图象,那么符合小明行驶情况的大致图象是()
A.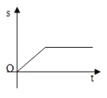 B.
B.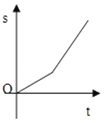 C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
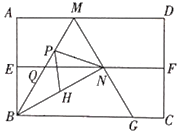
【题目】如图,四边形是矩形纸片,AB=2.对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q再次展平,连接BN,MN,延长MN交BC于点G.有如下结论:①∠ABN= 60°;②AM=1;③![]() ;④△BMG是等边三角形;⑤P为线段BM上一动点,H是BN的中点,则PN+PH的最小值是
;④△BMG是等边三角形;⑤P为线段BM上一动点,H是BN的中点,则PN+PH的最小值是![]() .其中正确结论的序号是___________.
.其中正确结论的序号是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一袋中装有形状大小都相同的四个小球,每个小球上各标有一个数字,分别是1,4,7,8.现规定从袋中任取一个小球,对应的数字作为一个两位数的个位数;然后将小球放回袋中并搅拌均匀,再任取一个小球,对应的数字作为这个两位数的十位数.
(1)写出按上述规定得到所有可能的两位数;
(2)从这些两位数中任取一个,求其算术平方根大于4且小于7的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com