
【题目】如图,点![]() 是线段
是线段![]() 上一点,
上一点,![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 的长为半径作⊙
的长为半径作⊙![]() ,过点
,过点![]() 作
作![]() 的垂线交⊙
的垂线交⊙![]() 于
于![]() ,
,![]() 两点,点
两点,点![]() 在线段
在线段![]() 的延长线上,连接
的延长线上,连接![]() 交⊙
交⊙![]() 于点
于点![]() ,以
,以![]() ,
,![]() 为边作
为边作![]() .
.

(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若![]() ,求四边形
,求四边形![]() 与⊙
与⊙![]() 重叠部分的面积;
重叠部分的面积;
(3)若![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 和
和![]() 的长.
的长.
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() :
:![]() 与直线
与直线![]() :
:![]() 且相交于点
且相交于点![]() ,直线
,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,直线
,直线![]() 与直线
与直线![]() ,
,![]() 分别相交于点
分别相交于点![]() 、
、![]() ,点
,点![]() 是线段
是线段![]() 的中点,以点
的中点,以点![]() 为顶点的抛物线
为顶点的抛物线![]() 经过点
经过点![]() .
.
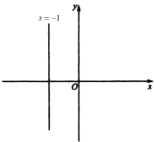
(1)①点![]() 的坐标是________;
的坐标是________;
②点![]() 的坐标是________.(用含
的坐标是________.(用含![]() 、
、![]() 的代数式表示)
的代数式表示)
(2)求![]() 的值(用含
的值(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
(3)若![]() ,当
,当![]() 时,
时,![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于![]() 的二次函数
的二次函数![]() .下列说法:①无论
.下列说法:①无论![]() 取何值,此二次函数图象与
取何值,此二次函数图象与![]() 必有两个交点;②无论
必有两个交点;②无论![]() 取何值,图象必过两定点,且两定点之间的距离为
取何值,图象必过两定点,且两定点之间的距离为![]() ;③当
;③当![]() 时,函数在
时,函数在![]() 时,
时,![]() 随
随![]() 的增大而减小;④当
的增大而减小;④当![]() 时,函数图象截
时,函数图象截![]() 轴所得的线段长度必大于2,其中结论正确的个数有 ( )
轴所得的线段长度必大于2,其中结论正确的个数有 ( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
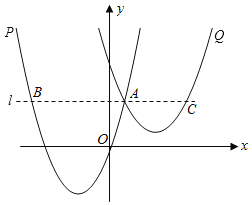
【题目】如图,抛物线P:![]() 与抛物线Q:
与抛物线Q:![]() 在同一平面直角坐标系中(其中a,t均为常数,且t>0),已知点A(1,3)为抛物线P上一点,过点A作直线l∥x轴,与抛物线P交于另一点B.
在同一平面直角坐标系中(其中a,t均为常数,且t>0),已知点A(1,3)为抛物线P上一点,过点A作直线l∥x轴,与抛物线P交于另一点B.
(1)求a的值及点B的坐标;
(2)当抛物线Q经过点A时
①求抛物线Q的解析式;
②设直线l与抛物线Q的另一交点为C,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
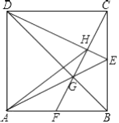
【题目】如图,正方形![]() 的边长为6,点
的边长为6,点![]() 是
是![]() 的中点,连接
的中点,连接![]() 与对角线
与对角线![]() 交于点
交于点![]() ,连接
,连接![]() 并延长,交
并延长,交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .以下结论:①
.以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
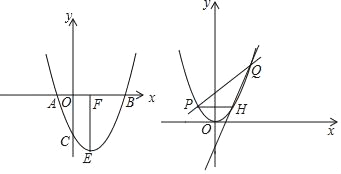
【题目】抛物线y=x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,﹣3).
(1)求抛物线的解析式;
(2)如图1,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.
(3)如图2,将抛物线平移,使其顶点E与原点O重合,直线y=kx+2(k>0)与抛物线相交于点P、Q(点P在左边),过点P作x轴平行线交抛物线于点H,当k发生改变时,请说明直线QH过定点,并求定点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
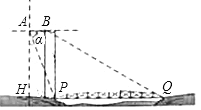
【题目】如图示一架水平飞行的无人机AB的尾端点A测得正前方的桥的左端点P的
俯角为α其中tanα=2![]() ,无人机的飞行高度AH为500
,无人机的飞行高度AH为500![]() 米,桥的长度为1255米.
米,桥的长度为1255米.
①求点H到桥左端点P的距离;
②若无人机前端点B测得正前方的桥的右端点Q的俯角为30°,求这架无人机的长度AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】事件发生的可能性有大有小,请你把下列事件发生可能性的大小按由小到大的顺序排列起来__________.(只排序号)
①书包里有12本不同科目的教科书,随手摸出一本,恰好是数学书;
②花2元买了一张彩票,就中了500万大奖;
③我抛了两次硬币,都正面向上;
④若![]() ,则
,则![]() 和
和![]() 互为相反数.
互为相反数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O为圆锥的顶点,M为圆锥底面上一点,点P在OM上.一只蜗牛从P点出发,绕圆锥侧面爬行,回到P点时所爬过的最短路线的痕迹如图所示.若沿OM将圆锥侧面剪开并展开,所得侧面展开图是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com