
【题目】如图示一架水平飞行的无人机AB的尾端点A测得正前方的桥的左端点P的
俯角为α其中tanα=2![]() ,无人机的飞行高度AH为500
,无人机的飞行高度AH为500![]() 米,桥的长度为1255米.
米,桥的长度为1255米.
①求点H到桥左端点P的距离;
②若无人机前端点B测得正前方的桥的右端点Q的俯角为30°,求这架无人机的长度AB.
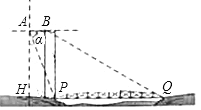
【答案】①求点H到桥左端点P的距离为250米;②无人机的长度AB为5米.
【解析】
试题分析:①在Rt△AHP中,由tan∠APH=tanα=![]() ,即可解决问题;②设BC⊥HQ于C.在Rt△BCQ中,求出CQ=
,即可解决问题;②设BC⊥HQ于C.在Rt△BCQ中,求出CQ=![]() =1500米,由PQ=1255米,可得CP=245米,再根据AB=HC=PH﹣PC计算即可;
=1500米,由PQ=1255米,可得CP=245米,再根据AB=HC=PH﹣PC计算即可;
试题解析:①在Rt△AHP中,∵AH=500![]() ,
,
由tan∠APH=tanα=![]() =2
=2![]() ,可得PH=250米.
,可得PH=250米.
∴点H到桥左端点P的距离为250米.
②设BC⊥HQ于C.
在Rt△BCQ中,∵BC=AH=500![]() ,∠BQC=30°,
,∠BQC=30°,
∴CQ=![]() =1500米,∵PQ=1255米,∴CP=245米,
=1500米,∵PQ=1255米,∴CP=245米,
∵HP=250米,∴AB=HC=250﹣245=5米.
答:这架无人机的长度AB为5米.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案科目:初中数学 来源: 题型:
【题目】(2015德阳)大华服装厂生产一件秋冬季外套需面料1.2米,里料0.8米,已知面料的单价比里料的单价的2倍还多10元,一件外套的布料成本为76元.
(1)求面料和里料的单价;
(2)该款外套9月份投放市场的批发价为150元/件,出现购销两旺态势,10月份进入批发淡季,厂方决定采取打折促销.已知生产一件外套需人工等固定费用14元,为确保每件外套的利润不低于30元.
①设10月份厂方的打折数为m,求m的最小值;(利润=销售价﹣布料成本﹣固定费用)
②进入11月份以后,销售情况出现好转,厂方决定对VIP客户在10月份最低折扣价的基础上实施更大的优惠,对普通客户在10月份最低折扣价的基础上实施价格上浮.已知对VIP客户的降价率和对普通客户的提价率相等,结果一个VIP客户用9120元批发外套的件数和一个普通客户用10080元批发外套的件数相同,求VIP客户享受的降价率.
查看答案和解析>>
科目:初中数学 来源: 题型:
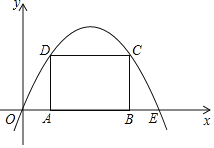
【题目】如图,抛物线y=ax2+bx(a<0)过点E(10,0),矩形ABCD的边AB在线段OE上(点A在点B的左边),点C,D在抛物线上.设A(t,0),当t=2时,AD=4.
(1)求抛物线的函数表达式.
(2)当t为何值时,矩形ABCD的周长有最大值?最大值是多少?
(3)保持t=2时的矩形ABCD不动,向右平移抛物线.当平移后的抛物线与矩形的边有两个交点G,H,且直线GH平分矩形的面积时,求抛物线平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区为方便游客参观,在每个景点均设置两条通道,即楼梯和无障碍通道.如图,已知在某景点P处,供游客上下的楼梯倾斜角为30°(即∠PBA=30°),长度为4m(即PB=4m),无障碍通道PA的倾斜角为15°(即∠PAB=15°).求无障碍通道的长度.(结果精确到0.1m,参考数据:sin15°≈0.21,cos15°≈0.98)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点(Brocard point)是法国数学家和数学教育家克洛尔(A.L.Crelle 1780﹣1855)于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡(Brocard 1845﹣1922)重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=( )
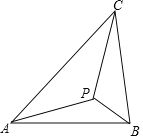
A.5 B.4 C.3+![]() D.2+
D.2+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG,EF与AD相交于点H,延长DA交GF于点K.若正方形ABCD边长为![]() ,则AK= .
,则AK= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象相交于点A(1,4)和点B(n,
的图象相交于点A(1,4)和点B(n,![]() ).
).
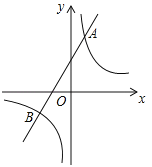
(1)求反比例函数和一次函数的解析式;
(2)当一次函数的值小于反比例函数的值时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组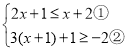 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得____________________;
(Ⅱ)解不等式②,得_______________________;
(III)把不等式①和②的解集在数轴上表示出来:

(IV)原不等式组的解集为________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点F,C是⊙O上两点,且![]() ,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
(1)求证:CD是⊙O的切线;
(2)若CD=2![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com