
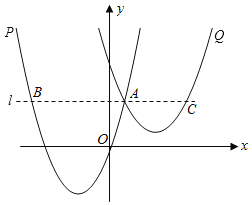
【题目】如图,抛物线P:![]() 与抛物线Q:
与抛物线Q:![]() 在同一平面直角坐标系中(其中a,t均为常数,且t>0),已知点A(1,3)为抛物线P上一点,过点A作直线l∥x轴,与抛物线P交于另一点B.
在同一平面直角坐标系中(其中a,t均为常数,且t>0),已知点A(1,3)为抛物线P上一点,过点A作直线l∥x轴,与抛物线P交于另一点B.
(1)求a的值及点B的坐标;
(2)当抛物线Q经过点A时
①求抛物线Q的解析式;
②设直线l与抛物线Q的另一交点为C,求![]() 的值.
的值.
【答案】(1)a=![]() ,B(﹣5,3);(2)①y2=
,B(﹣5,3);(2)①y2=![]() (x﹣3)2+1;②
(x﹣3)2+1;②![]() .
.
【解析】
(1)先利用待定系数法求出抛物线P的解析式,即可得出结论;
(2)①利用待定系数法求出抛物线Q的解析式,即可得出结论;
②先求出AC,AB,即可得出结论.
(1)∵抛物线P:y1=a(x+2)2﹣3过点A(1,3),∴9a﹣3=3,∴a![]() ,∴抛物线P:y1
,∴抛物线P:y1![]() (x+2)2﹣3.
(x+2)2﹣3.
∵l∥x轴,∴点B的纵坐标为3,∴3![]() (x+2)2﹣3,∴x=1(点A的横坐标)或x=﹣5,∴B(﹣5,3);
(x+2)2﹣3,∴x=1(点A的横坐标)或x=﹣5,∴B(﹣5,3);
(2)①如图,∵抛物线Q:y2![]() (x﹣t)2+1过点A(1,3),∴
(x﹣t)2+1过点A(1,3),∴![]() (1﹣t)2+1=3,∴t=﹣1(舍)或t=3,∴抛物线Q:y2
(1﹣t)2+1=3,∴t=﹣1(舍)或t=3,∴抛物线Q:y2![]() (x﹣3)2+1;
(x﹣3)2+1;
②∵l∥x轴,∴点C的纵坐标为3,∴3![]() (x﹣3)2+1,∴x=1(点A的横坐标)或x=5,∴C(5,1),∴AC=5﹣1=4.
(x﹣3)2+1,∴x=1(点A的横坐标)或x=5,∴C(5,1),∴AC=5﹣1=4.
∵A(1,3),B(﹣5,3),∴AB=1﹣(﹣5)=6,∴![]() .
.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠ACB=90°.
求作:射线CG,使得CG∥AB.
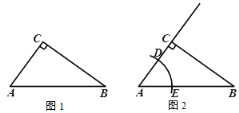
下面是小东设计的尺规作图过程.
作法:
①以点A为圆心,适当长为半径作弧,分别交AC,AB于D,E两点;
②以点C为圆心,AD长为半径作弧,交AC的延长线于点F;
③以点F为圆心,DE长为半径作弧,两弧在∠FCB内部交于点G;
④作射线CG.所以射线CG就是所求作的射线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接FG、DE.
∵△ADE ≌ △_________,
∴∠DAE = ∠_________.
∴CG∥AB(___________________)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为改善办学条件,计划购进![]() 两种规格的书架,经市场调查发现有线下和线上两种方式,具有情况如下表:
两种规格的书架,经市场调查发现有线下和线上两种方式,具有情况如下表:
规格 | 线下 | 线上 | ||
单价(元/个) | 运费(元/个) | 单价(元/个) | 运费(元/个) | |
A | 240 | 0 | 210 | 20 |
B | 300 | 0 | 250 | 30 |
(Ⅰ)如果在线下购买![]() 两种书架20个,共花费5520元,求
两种书架20个,共花费5520元,求![]() 两种书架各购买了多少个;
两种书架各购买了多少个;
(Ⅱ)如果在线上购买![]() 两种书架20个,共花费
两种书架20个,共花费![]() 元,设其中
元,设其中![]() 种书架购买
种书架购买![]() 个,求W关于
个,求W关于![]() 的函数关系式;
的函数关系式;
(Ⅲ)在(Ⅱ)的条件下,若购买![]() 种书架的数量不少于
种书架的数量不少于![]() 种书架的2倍,请求出花费最少的购买方案,并计算按照该购买方案线上比线下节约多少钱.
种书架的2倍,请求出花费最少的购买方案,并计算按照该购买方案线上比线下节约多少钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球多15元,王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?
(2)根据消费者需求,该网店决定用不超过8780元购进甲、乙两种羽毛球共200筒,且甲种羽毛球的数量大于乙种羽毛球数量的![]() ,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
①若设购进甲种羽毛球m筒,则该网店有哪几种进货方案?
②若所购进羽毛球均可全部售出,请求出网店所获利润W(元)与甲种羽毛球进货量m(筒)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
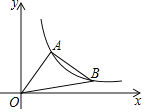
【题目】如图,横坐标为1的点A在反比例函数y=![]() 上(x>0)的图象上,将线段AO绕着点A逆时针旋转90°得到线段AB,且点B也落在反比例函数y=
上(x>0)的图象上,将线段AO绕着点A逆时针旋转90°得到线段AB,且点B也落在反比例函数y=![]() (x>0)的图象上
(x>0)的图象上
(1)求反比例函数的解析式;
(2)求线段AO扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 的中点,点
的中点,点![]() 在射线
在射线![]() 上,连接
上,连接![]() ,平移
,平移![]() ,使点
,使点![]() 移动到点
移动到点![]() ,得到
,得到![]() (点
(点![]() 与点
与点![]() 对应,点
对应,点![]() 与点
与点![]() 对应),
对应),![]() 交
交![]() 于点
于点![]() .
.
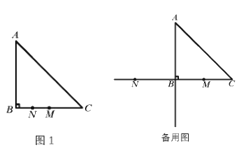
(1)若点![]() 是线段
是线段![]() 的中点,如图1.
的中点,如图1.
①依题意补全图1;
②求![]() 的长;
的长;
(2)若点![]() 在线段
在线段![]() 的延长线上,射线
的延长线上,射线![]() 与射线
与射线![]() 交于点
交于点![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是线段
是线段![]() 上一点,
上一点,![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 的长为半径作⊙
的长为半径作⊙![]() ,过点
,过点![]() 作
作![]() 的垂线交⊙
的垂线交⊙![]() 于
于![]() ,
,![]() 两点,点
两点,点![]() 在线段
在线段![]() 的延长线上,连接
的延长线上,连接![]() 交⊙
交⊙![]() 于点
于点![]() ,以
,以![]() ,
,![]() 为边作
为边作![]() .
.

(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若![]() ,求四边形
,求四边形![]() 与⊙
与⊙![]() 重叠部分的面积;
重叠部分的面积;
(3)若![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 和
和![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的有____(只填序号)
①非负数![]() 的平方根是非负数;
的平方根是非负数;
②已知圆锥的底面半径是![]() ,母线长是
,母线长是![]() ,则该圆锥的侧面积是
,则该圆锥的侧面积是![]() ;
;
③3是![]() 的平方根;
的平方根;
④若一组数据![]() 的众数是
的众数是![]() ,则中位数是
,则中位数是![]() ;
;
⑤任意三角形的外接圆的圆心一定是三角形三条边的垂直平分线的交点.
查看答案和解析>>
科目:初中数学 来源: 题型:
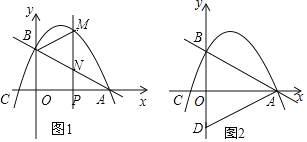
【题目】如图1,抛物线![]() (
(![]() )与
)与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线解析式和![]() 点坐标;
点坐标;
(2)在![]() 轴上有一动点
轴上有一动点![]() ,过点
,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() .当点
.当点![]() 位于第一象限图象上,连接
位于第一象限图象上,连接![]() ,求
,求![]() 面积的最大值及此时
面积的最大值及此时![]() 点的坐标;
点的坐标;
(3)如图2,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,连接
,连接![]() .
.
①点![]() 是线段
是线段![]() 上一点(不与点
上一点(不与点![]() 重合),点
重合),点![]() 是线段
是线段![]() 上一点(不与点
上一点(不与点![]() 重合),则两条线段之和
重合),则两条线段之和![]() 的最小值为 ;
的最小值为 ;
②将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() (
(![]() ),当点
),当点![]() 的对应点
的对应点![]() 落在
落在![]() 的边所在直线上时,则此时点
的边所在直线上时,则此时点![]() 的对应点
的对应点![]() 的坐标为 .
的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com