
【题目】如图,已知△ABC是等腰三角形,顶角∠BAC=![]() (
(![]() <600),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转
<600),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转![]() 到AE,过点E作BC的平行线,交AB于点F,连接DE、BE、DF
到AE,过点E作BC的平行线,交AB于点F,连接DE、BE、DF
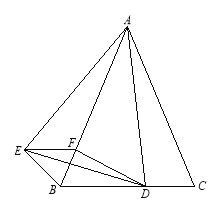
(1)求证:BE=CD
(2)若AD⊥BC,试判断四边形BDFE的形状,并给出证明。
【答案】见解析
【解析】
试题分析:根据旋转可得AE=AD,AB=AC,∠EAD=∠BAC,从而得到∠BAE=∠CAD,从而得出△ACD和△ABE全等,从而得出答案;根据题意得出△ABD和△ABE全等,从而得出∠EBF=∠DBF,根据EF∥BC得到∠DBF=∠EFB,从而得到∠EBF=∠EFB,则EB=EF,利用同理得出BD=FD,从而得到菱形.
试题解析:(1)∵△ABC是等腰三角形,顶角∠BAC=α(α<60°),线段AD绕点A顺时针旋转α到AE,∴AE=AD,AB=AC,∠EAD=∠BAC, ∴∠BAE=∠CAD
在△ACD和△ABE中 ∴△ACD≌△ABE(SAS) ∴BE=CD;
∴△ACD≌△ABE(SAS) ∴BE=CD;
(2)∵AD⊥BC,∴BD=CD,∠BAD=∠CAD, 由(1)可知,△ACD≌△ABE,∴BE=BD=CD,∠BAE=∠BAD
在△ABD和△ABE中,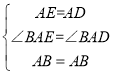 ∴△ABD≌△ABE(SAS), ∴∠EBF=∠DBF,
∴△ABD≌△ABE(SAS), ∴∠EBF=∠DBF,
∵EF∥BC, ∴∠DBF=∠EFB, ∴∠EBF=∠EFB, ∴EB=EF,同理BD=FD,∴BD=BE=EF=FD,
∴四边形BDFE为菱形


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】如图,已知等腰△ABC顶角∠A=36°.
(1)尺规作图:在AC上作一点D,使AD=BD;(保留作图痕迹,不必写作法和证明)
(2)求证:△BCD是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①a<0;② ![]() =1;③b2﹣4ac<0;④当x>1时,y随x的增大而减小;⑤当﹣1<x<3时,y<0,其中正确的是_____.(只填序号)
=1;③b2﹣4ac<0;④当x>1时,y随x的增大而减小;⑤当﹣1<x<3时,y<0,其中正确的是_____.(只填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点D为△ABC内的一点,∠ADB=120°,∠ADC=90°,将△ABD绕点A逆时针旋转60°得△ACE,连接DE.
(1)求证:AD=DE;
(2)求∠DCE的度数;
(3)若BD=1,求AD,CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,EF//AD,∠1=∠2,∠BAC=70°,请将求∠AGD 的过程补充完整.

解:∵EF//AD
∴∠2= ( )
∵∠1=∠2 ∴∠1=∠3 ( )
∴AB// ![]() ( )
( )
∴∠BAC+ =180° ( )
∵∠BAC=70° ∴∠AGD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解下列方程:
(1)4x2 -4x -1 = 0; (2)7x2 -28x +7= 0.
(3) ![]() x2-x-4=0 (4) 3x2-45=30x
x2-x-4=0 (4) 3x2-45=30x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乐乐和科学小组的同学们在网上获取了声音在空气中传播的速度与空气温度之间关系的一些数据(如下表)
温度/ | -20 | -10 | 0 | 10 | 20 | 30 |
声速/( | 318 | 324 | 330 | 336 | 342 | 348 |
下列说法中错误的是( )
A.在这个变化过程中,当温度为10![]() 时,声速是336
时,声速是336![]()
B.温度越高,声速越快
C.当空气温度为20![]() 时,声音5
时,声音5![]() 可以传播1740
可以传播1740![]()
D.当温度每升高10![]() ,声速增加6
,声速增加6![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?

(3)在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少127.5元,则第15天在第14天的价格基础上最多可降多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com