
【题目】如图,在菱形ABCD中,AB=BD,点E,F分别在BC,CD边上,且CE=DF,BF与DE交于点G,若BG=2,DG=4,则CD长为__.

【答案】2![]()
【解析】延长DE至H,使GH=BG,连接BH、CH,∵四边形ABCD为菱形,∴BC=DC=AB=BD,∴△BDC是等边三角形,∴∠DBC=∠BCF=60°,∵CE=DF,∴BC﹣CE=CD﹣DF,即BE=CF,在△DBE和△BCF中,∵DB=BC,∠DBC=∠BCF,BE=CF,∴△DBE≌△BCF(SAS),∴∠BDG=∠FBC,∴∠BDG+∠DBF=∠FBC+∠DBF=60°,∴∠BGE=∠BDG+∠DBF=60°,∴△BGH为等边三角形,∴BG=BH=2,∠GBH=60°,∴∠DBF+∠FBC=∠HBC+∠FBC,∴∠DBF=∠HBC,在△BGD和△BHC中,∵BD=BC,∠DBF=∠HBC,BG=BH,∴△BGD≌△BHC(SAS),∴DG=CH=4,∵∠FBC=∠BDG=∠BCH,∴BF∥CH,∴△BGE∽△CEH,∴ ![]() ,∵EG+EH=2,∴EG=
,∵EG+EH=2,∴EG=![]() ,∴BF=DE=4+
,∴BF=DE=4+![]() =
=![]() ,∵∠FBC=∠FBC,∠BGE=∠BCD=60°,∴△BGE∽△BCF,∴
,∵∠FBC=∠FBC,∠BGE=∠BCD=60°,∴△BGE∽△BCF,∴![]() ,∴
,∴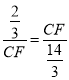 ,∴CF2=
,∴CF2=![]() ,CF=
,CF=![]() ,∴BE=CF=
,∴BE=CF=![]() ,∴BC=3BE=3×
,∴BC=3BE=3×![]() =
=![]() ,∴CD=BC=
,∴CD=BC=![]() .
.
故答案为: ![]() .
.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在2016年泉州市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
A. 平均数为160 B. 中位数为158 C. 众数为158 D. 方差为20.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等腰三角形,顶角∠BAC=![]() (
(![]() <600),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转
<600),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转![]() 到AE,过点E作BC的平行线,交AB于点F,连接DE、BE、DF
到AE,过点E作BC的平行线,交AB于点F,连接DE、BE、DF
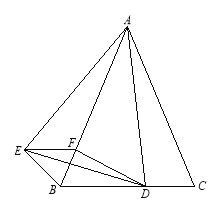
(1)求证:BE=CD
(2)若AD⊥BC,试判断四边形BDFE的形状,并给出证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面解答过程,并填空或在括号内填写理由.
已知BE平分∠ABC交AC于点E,DE∥BC,且∠ABC=110°,![]() ,请说明BE⊥AC.
,请说明BE⊥AC.

解:∵![]() 平分
平分![]() (已知),
(已知),
∴∠EBC=![]() ∠_______(角平分线定义).
∠_______(角平分线定义).
∵![]() ,
,
∴∠EBC=_______![]() .
.
∵![]() ∥
∥![]() ,
,![]() (已知),
(已知),
∴∠EBC=∠_______(两直线平行,内错角相等),
∠C=∠AED=35° (________).
∴∠AEB=∠______+∠______=90°.
∴![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B.
(1)求一次函数的解析式;
(2)判断点C(4,-2)是否在该一次函数的图象上,说明理由;
(3)若该一次函数的图象与x轴交于D点,求△BOD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
(1)当x≥30,求y与x之间的函数关系式;
(2)若小李4月份上网20小时,他应付多少元的上网费用?
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A的坐标是(a,0),点B的坐标是(b,0),其中a,b满足![]() .
.
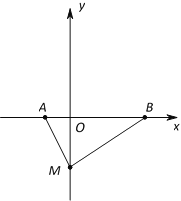
(1)填空:a=______,b=_______;
(2)在![]() 轴负半轴上有一点M(0,m),三角形ABM的面积为4.
轴负半轴上有一点M(0,m),三角形ABM的面积为4.
①求m的值;
②将线段AM沿x轴正方向平移,使得A的对应点为B,M的对应点为N. 若点P为线段AB上的任意一点(不与A,B重合),试写出∠MPN,∠PMA,∠PNB之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在CB的延长线上,点F在DE的延长线上,连接AF,分别与BD、CE交于点G、H。已知∠1=52°,∠2=128°。
(1)求证:BD∥CE;
(2)若∠A=∠F,试判断∠C与∠D的数量关系,并说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种产品的成本为30元/件,且年销售量y(万件)关于售价x(元/件)的函数解析式为:
![]()
(1)若企业销售该产品获得的利润为W(万元),请直接写出年利润W(万元)关于售价x(元/件)的函数解析式;
(2)当该产品的售价x(元/件)为多少时,企业销售该产品获得的年利润最大?最大年利润是多少?
(3)若企业销售该产品的年利润不少于750万元,试确定该产品的售价x(元/件)的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com