
【题目】某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种产品的成本为30元/件,且年销售量y(万件)关于售价x(元/件)的函数解析式为:
![]()
(1)若企业销售该产品获得的利润为W(万元),请直接写出年利润W(万元)关于售价x(元/件)的函数解析式;
(2)当该产品的售价x(元/件)为多少时,企业销售该产品获得的年利润最大?最大年利润是多少?
(3)若企业销售该产品的年利润不少于750万元,试确定该产品的售价x(元/件)的取值范围.
【答案】(1)年利润W(万元)关于售价x(元/件)的函数解析式为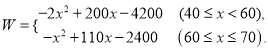 ;
;
(2)当该产品的售价定为50元/件时,销售该产品的年利润最大,最大利润为800万元;
(3)要使企业销售该产品的年利润不少于750万元,该产品的销售价x(元/件)的取值范围为45≤x≤55.
【解析】(1)根据:年利润=(售价﹣成本)×年销售量,结合x的取值范围可列函数关系式;
(2)将(1)中两个二次函数配方后依据二次函数的性质可得其最值情况,比较后可得答案;
(3)根据题意知W≥750,可列关于x的不等式,求解可得x的范围.
解:(1) 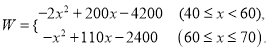
(2)由(1)知,当40≤x<60时, ![]() .
.
∵-2<0,∴当x=50时,W有最大值800.
当60≤x≤70时, ![]() .
.
∵-1<0, ∴当60≤x≤70时,W随x的增大而减小.
∴当x=60时,W有最大值600.
![]()
∴当该产品的售价定为50元/件时,销售该产品的年利润最大,最大利润为800万元.
(3)当40≤x<60时,令W=750,得
-2(x-50)2+800=750,解之,得![]()
由函数![]() 的性质可知,
的性质可知,
当45≤x≤55时,W≥750.
当60≤x≤70时,W最大值为600<750.
所以,要使企业销售该产品的年利润不少于750万元,该产品的销售价x(元/件)的取值范围为45≤x≤55.
“点睛”本题主要考查二次函数的实际应用,梳理题目中的数量关系,得出相等关系后分情况列出函数解析式,熟练运用二次函数性质求最值是解题的关键.


科目:初中数学 来源: 题型:
【题目】某校分别与2014年、2015年随机调查相同数量的学生,对数学开展小组合作学习的情况进行调查(开展情况分为较少、有时、常常、总是四种),绘制成部分统计图如下.请根据图中信息,解答下列问题: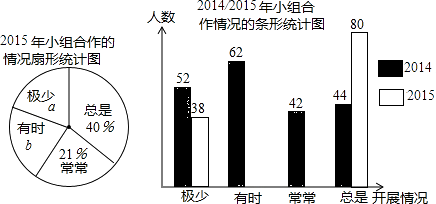
(1)求:2015年随机调查抽取的学生数量;
(2)直接写出a,b的结果:a= , b=;
(3)计算:“总是”对应的圆心角度数;
(4)请你补全条形统计图;
(5)相比2014年,2015年数学课开展小组合作学习的情况有何变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 ![]() 中,直线
中,直线 ![]() 与直线
与直线 ![]() 相交于点A(2,4),直线
相交于点A(2,4),直线 ![]() 与x轴交于点B(6,0).
与x轴交于点B(6,0).
(1)分别求直线 ![]() 和
和 ![]() 的表达式;
的表达式;
(2)过动点P(0,n)且垂直于 ![]() 轴的直线与
轴的直线与 ![]() ,
, ![]() 的交点分别为C , D , 当点C 位于点D左方时,请直接写出n的取值范围.
的交点分别为C , D , 当点C 位于点D左方时,请直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一元二次方程x2﹣2x﹣1=0的两个根为m、n,则一次函数y=(m+n)x+mn的图象不经过( )
A.第一象限B.第二象限C.第三象限D.第四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x,y为有理数,现规定一种运算“*”,满足x*y=xy+1(等式中xy表示x与y的积)
(1)求2*4的值;
(2)求(1*4)*(﹣2).
查看答案和解析>>
科目:初中数学 来源: 题型:
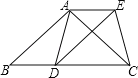
【题目】已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.
(1)求证:AD=CE;
(2)当点D在什么位置时,四边形ADCE是矩形,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com