
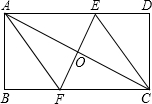
 如图,已知四边形ABCD是矩形,对角线AC的垂直平分线交AD于点E,交BC于点F,连接AF,CE,解答下列问题:
如图,已知四边形ABCD是矩形,对角线AC的垂直平分线交AD于点E,交BC于点F,连接AF,CE,解答下列问题:分析 (1)由ASA证明△AOE≌△COF,得出对应边相等EO=FO,证出四边形AFCE为平行四边形,再由FE⊥AC,即可得出结论.
(2)由勾股定理和根与系数的关系得出方程,解方程求出m=1或m=-5,再由根的判别式即可得出m的值.
解答 (1)证明:∵四边形ABCD是矩形,
∴AE∥FC,
∴∠EAO=∠FCO,
∵EF垂直平分AC,
∴AO=CO,FE⊥AC,
在△AOE和△COF中,$\left\{\begin{array}{l}{∠EAO=∠FCO}&{\;}\\{AO=CO}&{\;}\\{∠AOE=∠COF}&{\;}\end{array}\right.$,
∴△AOE≌△COF(ASA),
∴EO=FO,
∴四边形AFCE为平行四边形,
又∵FE⊥AC,
∴平行四边形AECF为菱形.
(2)解:在△ABF中,∵∠ABF=90°,
∴AB2+BF2=AF2,
∴AF2=a2+b2=(a+b)2-2ab,
由根与系数的关系得:a+b=2(m+1),ab=m2+1,
∴AF2=[2(m+1)]2-2(m2+1)=2m2+8m+2,
∵菱形AECF的周长为8$\sqrt{3}$,
∴AF=2$\sqrt{3}$,
∴2m2+8m+2=(2$\sqrt{3}$)2,
解得:m=1或m=-5,
∵原方程有实数根,则△≥0,
∴[-2(m+1)]2-4(m2+1)≥0,
∴m=-5不合题意,舍去,
∴m=1,
即当m=1时,菱形AECF的周长为8$\sqrt{3}$.
点评 本题考查了矩形的性质、菱形的判定方法、平行四边形的判定方法、全等三角形的判定与性质、勾股定理、根与系数的关系以及根的判别式;熟练掌握矩形的性质,证明三角形全等是解决问题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 5 | C. | 1或5 | D. | 无法计算 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
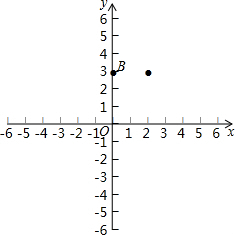 已知抛物线y=ax2+bx+c的顶点为A,经过点B(0,3)和点(2,3),与x轴交于C,D两点,(点C在点D的左侧),且OD=OB.
已知抛物线y=ax2+bx+c的顶点为A,经过点B(0,3)和点(2,3),与x轴交于C,D两点,(点C在点D的左侧),且OD=OB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
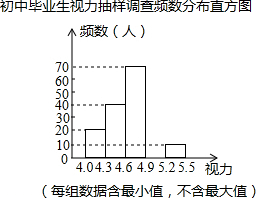 某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和不完整的频数分布直方图,请根据图表信息回答下列问题:
某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和不完整的频数分布直方图,请根据图表信息回答下列问题:| 视力 | 频数(人) | 频率 |
| 4.0≤x<4.3 | 20 | 0.1 |
| 4.3≤x<4.6 | 40 | 0.2 |
| 4.6≤x<4.9 | 70 | 0.35 |
| 4.9≤x<5.2 | a | 0.3 |
| 5.2≤x<5.5 | 10 | b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com