
分析 (1)只需运用直接开平方法即可解决问题;
(2)只需运用配方法即可解决问题;
(3)只需运用因式分解法即可解决问题;
(4)只需运用因式分解法即可解决问题.
解答 解:(1)原方程可转化为
x2=25,
解得:x1=5,x2=-5;
(2)原方程可转化为
x2-6x+9=0,
配方得(x-3)2=0,
解得:x1=x2=3;
(3)原方程可转化为
(x-1)2-2x(x-1)=0,
即(x-1)(x-1-2x)=0,
也即(x-1)(-x-1)=0,
解得:x1=1,x2=-1;
(4)原方程可转化为
x2+x-12=0,
即(x+4)(x-3)=0,
解得:x1=-4,x2=3.
点评 本题主要考查的是运用适当的方法解一元二次方程,解一元二次方程通常有四种方法(直接开平方法、因式分解法、配方法、公式法),通常可根据一元二次方程的特点选择相应的方法.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | ±1 | D. | -$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
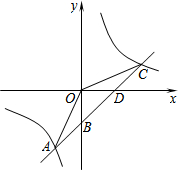 如图,一次函数y=kx+b的图象与反比例函数$y=\frac{m}{x}$的图象交于点A﹙-2,-5﹚,C﹙5,n﹚,交y轴于点B,交x轴于点D.
如图,一次函数y=kx+b的图象与反比例函数$y=\frac{m}{x}$的图象交于点A﹙-2,-5﹚,C﹙5,n﹚,交y轴于点B,交x轴于点D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在菱形ABCD中,EF⊥AC于点G,分别交AD及CB的延长线于点E、F交AB于点H,AH:FB=1:2,则AG:GC的值为( )
如图,在菱形ABCD中,EF⊥AC于点G,分别交AD及CB的延长线于点E、F交AB于点H,AH:FB=1:2,则AG:GC的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com