
����Ŀ����ͼ1����P��Q�ֱ��DZ߳�Ϊ4cm�ĵȱ���ABC��AB��BC�ϵĶ��㣬��P�Ӷ���A����Q�Ӷ���Bͬʱ�����������ǵ��ٶȶ�Ϊ1cm/s��
��1������AQ��CP���ڵ�M������P��Q�˶��Ĺ����У���CMQ�仯�����仯����˵�����ɣ������䣬��������Ķ�����
��2�������ʱ��PBQ��ֱ�������Σ�
��3����ͼ2������P��Q���˶����յ�����������AB��BC���˶���ֱ��AQ��CP����ΪM������CMQ�仯�����仯����˵�����ɣ������䣬��������Ķ�����

���𰸡���1����P��Q�˶��Ĺ����У���CMQ���䣬��CMQ=60�㣻��2����tΪ![]() s��
s��![]() s ʱ����PBQΪֱ�������Σ���3����P��Q�˶��Ĺ����У���CMQ�Ĵ�С���䣬��CMQ=120�㣮
s ʱ����PBQΪֱ�������Σ���3����P��Q�˶��Ĺ����У���CMQ�Ĵ�С���䣬��CMQ=120�㣮
�������������������1�����õȱ������ε����ʿ�֤����APC�ա�BQA�������á�BAQ=��ACP����������������ǵ����ʿ�֤�á�CMQ=60�㣻
��2������t�ֱ��ʾ��BP��BQ���֡�BPQ=90��͡�BPQ=90������������ֱ�����ֱ�������ε����ʿɵõ�����t�ķ��̣�������t��ֵ��
��3��ͬ��1����֤�á�PBC�ա�QCA����������������ǵ����ʿ���á�CMQ=120�㣮
�����������1���ߡ�ABCΪ�ȱ������Σ�
��AB=AC����B=��PAC=60�㣬
�ߵ�P�Ӷ���A����Q�Ӷ���Bͬʱ�����������ǵ��ٶȶ�Ϊ1cm/s��
��AP=BQ��
�ڡ�APC�͡�BQA��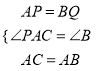 ��
��
���APC�ա�BQA��SAS����
���BAQ=��ACP��
���CMQ=��CAQ+��ACP=��BAQ+��CAQ=��BAC=60�㣬
����P��Q�˶��Ĺ����У���CMQ���䣬��CMQ=60�㣻
��2�����˶�ʱ��Ϊts����AP=BQ=t��
��PB=4��t��
����PQB=90��ʱ��
�ߡ�B=60�㣬
��PB=2BQ��
��4��t=2t�����t=![]() ��
��
����BPQ=90��ʱ��
�ߡ�B=60�㣬
��BQ=2PB��
��t=2��4��t�������t=![]() ��
��
�൱tΪ![]() s��
s��![]() s ʱ����PBQΪֱ�������Σ�
s ʱ����PBQΪֱ�������Σ�
��3���ڵȱ�������ABC�У�AC=BC����ABC=��BCA=60�㣬
���PBC=��QCA=120������BP=CQ��
�ڡ�PBC�͡�QCA��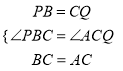 ��
��
���PBC�ա�QCA��SAS����
���BPC=��MQC��
�֡ߡ�PCB=��MCQ��
���CMQ=��PBC=120�㣬
����P��Q�˶��Ĺ����У���CMQ�Ĵ�С���䣬��CMQ=120�㣮


 ����ѧ��Ӯ�����ϵ�д�
����ѧ��Ӯ�����ϵ�д� ѧ���쳵�����ּ��������ҵ�½����������ϵ�д�
ѧ���쳵�����ּ��������ҵ�½����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ξ��ж����β����е������ǣ� ��
A.�Ա����B.�Խ�����ƽ��C.�Խ����ഹֱD.�Խ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
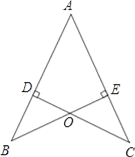
����Ŀ����ͼ��AB=AC��CD��AB��D��BE��AC��E��BE��CD�ཻ�ڵ�O��
��1����֤��AD=AE��
��2������OA��BC�����ж�ֱ��OA��BC�Ĺ�ϵ��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������x�ķ���x2+k2��16��0��x2��3k+12��0����ͬ��ʵ��������ôk��ֵ�ǣ�������
A.��7B.��7��4C.7D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������̨�����Ǽ�������ǣ� ��
A.ͬ���ڽǻ�������ֱ��ƽ��
B.��ͬһƽ���ڣ���ֱ��a��b����a��b�ཻ���ɵĽ�Ϊֱ��
C.��������ǻ�������ô����������һ����ǣ�һ���۽�
D.ƽ����ͬһ��ֱ�ߵ�����ֱ��ƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�����߳�Ϊ4��5������ʹ��ABC��ֱ�������εĵ����ߵ�ƽ����(����)
A.9B.41C.3D.9��41
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������У��Ǽ�������ǣ� ��
A.ƽ���ı��ε�����Ա߷ֱ����B.����Ա߷ֱ���ȵ��ı�����ƽ���ı���
C.���εĶԽ������D.�Խ�����ȵ��ı����Ǿ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����a��b��Ϊ�෴��, c����С�ķǸ���, d����С��������, ��(a+b)d+d��c��ֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com