
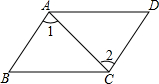
 如图,AB∥CD,AB=CD.问:△ABC和△CDA是全等三角形吗?为什么?
如图,AB∥CD,AB=CD.问:△ABC和△CDA是全等三角形吗?为什么?科目:初中数学 来源: 题型:
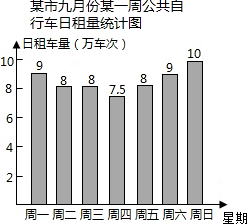 作为某市政府民生实事之一的公共自行车建设工作已基本完成,某部门对2014年九月份中的7天进行了公共自行车日租车量的统计,结果如图:
作为某市政府民生实事之一的公共自行车建设工作已基本完成,某部门对2014年九月份中的7天进行了公共自行车日租车量的统计,结果如图:查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC中,∠B的平分线与∠C的外角的平分线交于P点,PD⊥AC于D,PH⊥BA于H,
如图,△ABC中,∠B的平分线与∠C的外角的平分线交于P点,PD⊥AC于D,PH⊥BA于H,查看答案和解析>>
科目:初中数学 来源: 题型:
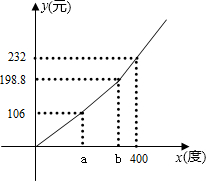 自2012年6月1日起,全国实施了阶梯电价.某省出台了阶梯电价方案:电价分“三档”收费,第一档为a度,居民用电量低于a度的部分,执行现行的标准电价(0.53元/度);第二档为a~b度,居民月用电量在a~b之间的部分,电价在一档电价的基础上提高0.05元/度;第三档为超过b度,居民月用电量高于b度的部分,电价在一档电价的基础上提高m元/度.实施阶梯电价后,月电费y(元)与月用电量x(度)之间的函数关系如图所示.
自2012年6月1日起,全国实施了阶梯电价.某省出台了阶梯电价方案:电价分“三档”收费,第一档为a度,居民用电量低于a度的部分,执行现行的标准电价(0.53元/度);第二档为a~b度,居民月用电量在a~b之间的部分,电价在一档电价的基础上提高0.05元/度;第三档为超过b度,居民月用电量高于b度的部分,电价在一档电价的基础上提高m元/度.实施阶梯电价后,月电费y(元)与月用电量x(度)之间的函数关系如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com