Question

【题目】如图，△ABC和△ECD都是等腰直角三角形，∠ACB=∠DCE=∠90°，D为AB边上一点．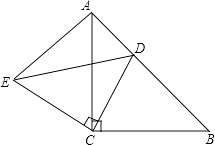
（1）求证：△ACE≌△BCD；
（2）若AD=6，BD=8，求ED的长．

Answer 1

【答案】
（1）证明：∵△ABC和△ECD都是等腰直角三角形，∠ACB=∠DCE=∠90°，

∴AC=BC，EC=DC，∠B=∠CAB=45°，∠ACE=∠BCD=90°﹣∠ACD，

在△ACE和△BCD中

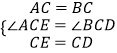
∴△ACE≌△BCD（SAS）；

（2）解：∵△ACE≌△BCD，

∴∠CAE=∠B，AE=BD=8，

∵∠CAB=∠B=45°，

∴∠EAD=45°+45°=90°，

在Rt△EAD中，由勾股定理得：ED= = =10．

【解析】（1）根据等腰直角三角形性质求出AC=BC，EC=DC，∠B=∠CAB=45°，求出∠ACE=∠BCD=90°﹣∠ACD，根据全等三角形的判定推出即可．（2）根据全等推出∠CAE=∠B，AE=BD=8，求出∠EAD=90°，根据勾股定理求出即可．
【考点精析】关于本题考查的等腰直角三角形，需要了解等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°才能得出正确答案．