【题目】解不等式（组），并把它们的解集在数轴上表示出来．
（1）
﹣2＞ 
（2）
．
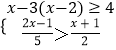【答案】
（1）
解：去分母，得：2（5x+1）﹣24＞3（x﹣5），
去括号，得：10x+2﹣24＞3x﹣15，
移项，得：10x﹣3x＞﹣15﹣2+24，
合并同类项，得：7x＞7，
系数化为1，得：x＞1；
将解集表示在数轴上如下：
（2）
解：解不等式x﹣3（x﹣2）≥4，得：x≤1，
解不等式 
＞ 
，得：x＜﹣7，
∴不等式组的解集为：x＜﹣7，
将解集表示在数轴上如下：
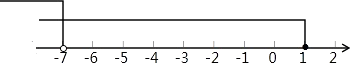
【解析】（1）根据解一元一次不等式基本步骤：去分母、去括号、移项、合并同类项、系数化为1可得；（2）分别求出每一个不等式的解集，根据口诀：“同小取小”确定不等式组的解集．
【考点精析】关于本题考查的不等式的解集在数轴上的表示和一元一次不等式的解法，需要了解不等式的解集可以在数轴上表示，分三步进行：①画数轴②定界点③定方向．规律：用数轴表示不等式的解集，应记住下面的规律：大于向右画，小于向左画，等于用实心圆点，不等于用空心圆圈；步骤：①去分母；②去括号；③移项；④合并同类项； ⑤系数化为1（特别要注意不等号方向改变的问题）才能得出正确答案．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】如图，△ABC是等腰三角形，AB=BC，点D为BC的中点．
（1）用圆规和没有刻度的直尺作图，并保留作图痕迹：
①过点B作AC的平行线BP；
②过点D作BP的垂线，分别交AC，BP，BQ于点E，F，G．
（2）在（1）所作的图中，连接BE，CF．求证：四边形BFCE是平行四边形．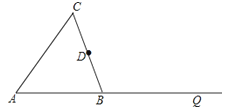
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，点C沿着某条路径运动，以点C为旋转中心，将点A(0，4)逆时针方向旋转60°，到点B(m，1)．若－5≤m≤5，则点C的运动路径长为___________.
查看答案和解析>>
科目：初中数学 来源： 题型：
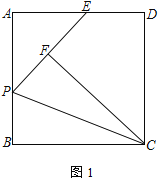
【题目】如图，正方形ABCD中，点P为AB边上一点，将△BCP沿CP翻折至△FCP位置，延长至PF交边AD于E点.
(1) 求证：EF＝DE.
(2) 若DF延长线与CP延长线交于G点，求
的值.
(3) 在(2)的条件下，若正方形的边长为
， 
，直接写出DG的长为___________.
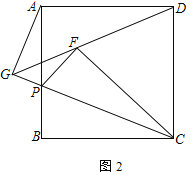
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，坡面CD的坡比为
，坡顶的平地BC上有一棵小树AB，当太阳光线与水平线夹角成60°时，测得小树的在坡顶平地上的树影BC是3米，斜坡上的树影CD是
米，则小树AB的高是 米.
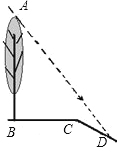
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC和△ECD都是等腰直角三角形，∠ACB=∠DCE=∠90°，D为AB边上一点．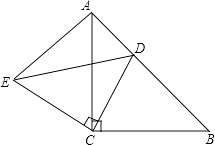 
（1）求证：△ACE≌△BCD；
（2）若AD=6，BD=8，求ED的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知在Rt△ABC中，∠ABC=90°，点D沿BC自B向C运动（点D与点B、C不重合），作BE⊥AD于E，CF⊥AD于F，则BE+CF的值（ ）
A．不变 B．增大 C．减小 D．先变大再变小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com