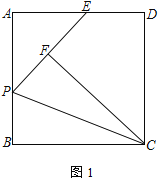
【题目】如图，正方形ABCD中，点P为AB边上一点，将△BCP沿CP翻折至△FCP位置，延长至PF交边AD于E点.

(1) 求证：EF＝DE.

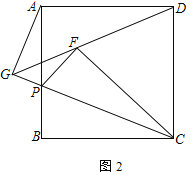
(2) 若DF延长线与CP延长线交于G点，求的值.

(3) 在(2)的条件下，若正方形的边长为， ，直接写出DG的长为___________.

参考答案：

【答案】(1)证明见解析;(2) ;(3)

【解析】试题分析：(1) 连接CE，利用HL判定三角形全等，得出结论即可.

(2) 过点A作AM⊥DG于M，过点C作CN⊥DG于N. 可得△CNG为等腰直角三角形，GM＝DN＝AM.△AGM为等腰直角三角形，AG＝AM＝DF， .

(3) 由AB＝， 得BP＝，AP＝，再由勾股定理和相似得， ，由对角互补四边形模型可知：AG＋GC＝DG，可得DG＝.

试题解析：

(1) 连接CE

∵∠CFE＝∠CDE＝90°，BC＝CF＝CD

∴Rt△CFE≌Rt△CDE（HL）

∴EF＝DE

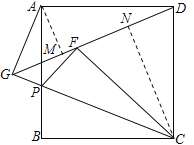
(2) 过点A作AM⊥DG于M，过点C作CN⊥DG于N

∴△AMD≌△DNC（AAS）

∴AM＝DN，DM＝CN

∵CF＝CD

∴∠FCN＝∠DCN

又∠BCP＝∠FCP

∴∠NCP＝45°

∴△CNG为等腰直角三角形

∴GN＝CN＝DM

∴GM＝DN＝AM

∴△AGM为等腰直角三角形

∴AG＝AM＝DF

∴

(3) ∵AB＝，

∴BP＝，AP＝

在Rt△BCP中，

∵Rt△GAP∽Rt△BCP

∴

即，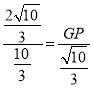

在Rt△AGP中，

由对角互补四边形模型可知：AG＋GC＝DG

∴DG＝

关闭