
����Ŀ�����κ���y=ax2+bx+c��a��0���IJ���ͼ����ͼ��ͼ����㣨��1��0�����Գ���Ϊֱ��x=2�����н��ۣ�
��4a+b=0����9a+c��3b����8a+7b+2c��0������x����1ʱ��y��ֵ��xֵ�������������������ֵy<0ʱ���Ա���x��ȡֵ��Χ��x<-1��x>5.
������ȷ�Ľ����У�������

A. 2�� B. 3�� C. 4�� D. 5��
���𰸡�B
��������
����������١������ߵĶԳ���Ϊֱ��x=-![]() =2��
=2��
��b=-4a����4a+b=0���ʱ�������ȷ��
�ڡ���x=-3ʱ��y��0��
��9a-3b+c��0��
��9a+c��3b���ʱ����۴���
�ۡ���������x���һ������Ϊ��-1��0����
��a-b+c=0��
��b=-4a��
��a+4a+c=0����c=-5a��
��8a+7b+2c=8a-28a -10a =-30a��
�������߿������£�
��a��0��
��8a+7b+2c��0���ʱ�������ȷ��
�ܡ��Գ���Ϊֱ��x=2��
����-1��x��2ʱ��y��ֵ��xֵ�����������
��x��2ʱ��y��x���������С���ʱ����۴���
�ݡ������ߵĶԳ���Ϊֱ��x=2����x���һ������Ϊ��-1��0����
����������x�������һ������Ϊ��5��0����
��������ֵy��0ʱ���Ա���x��ȡֵ��Χ��x��-1��x��5���ʱ�������ȷ��
��ѡB��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�մɹ�˾�й����ƣ�������˾���˹���ʱ�䣺ÿ�칤��![]() Сʱ��ÿ�¹���
Сʱ��ÿ�¹���![]() �죻���������˰��Ƽ������ʣ�ÿ�����������
�죻���������˰��Ƽ������ʣ�ÿ�����������![]() Ԫ�����½����������ù�˾ֻ�����ס��������մɣ�����С����¼������һЩ���ݣ�
Ԫ�����½����������ù�˾ֻ�����ס��������մɣ�����С����¼������һЩ���ݣ�
�����մ� ����λ������ | �����մ� ����λ������ | ��ʱ�� ����λ�����ӣ� | �Ƽ����� ����λ��Ԫ�� |
|
|
|
|
|
|
|
|
��1��������ÿ�������մ������ʱ��Ϊ![]() ���ӣ��ú���
���ӣ��ú���![]() �Ĵ���ʽ��ʾ����ÿ�������մ������ʱ�䣻
�Ĵ���ʽ��ʾ����ÿ�������մ������ʱ�䣻
��2����С������С��ij�£�����![]() �죩���������մ�
�죩���������մ�![]() ���������մ�
���������մ�![]() ����
����
������![]() ��
��![]() �ĺ�����ϵʽ��������д���Ա���
�ĺ�����ϵʽ��������д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�ڸ����г����飬ÿ������ÿ�����������մɵ����������������մ�������![]() ����������ÿ�������մɵļƼ����ʿ����
����������ÿ�������մɵļƼ����ʿ����![]() Ԫ�������մɼƼ�����Ҳ����ߵĿռ䣮��С���Ĺ���Ч�ʲ��䣬�����մɼƼ���������Ҫ��߶���Ԫ��С�����¹��ʣ��Ƽ�����+��������
Ԫ�������մɼƼ�����Ҳ����ߵĿռ䣮��С���Ĺ���Ч�ʲ��䣬�����մɼƼ���������Ҫ��߶���Ԫ��С�����¹��ʣ��Ƽ�����+��������![]() �¹��ʣ������쵽
�¹��ʣ������쵽![]() Ԫ��
Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ���ڵ�����ֱ�����ཻ��ƽ������λ�ù�ϵ
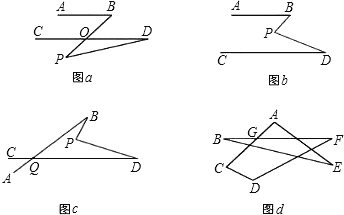
��1����ͼa����AB��CD����P��AB��CD�ⲿ�����С�B����BOD�������BOD�ǡ�POD����ǣ��ʡ�BOD����BPD+��D���á�BPD����B����D������P�Ƶ�AB��CD�ڲ�����ͼb�����Ͻ����Ƿ��������������˵�����ɣ��������������BPD����B����D֮���к�������ϵ����֤����Ľ��ۣ�
��2����ͼb�У���ֱ��AB�Ƶ�B��ʱ�뷽����תһ���ǶȽ�ֱ��CD�ڵ�Q����ͼc�����BPD����B����D����BQD֮���к�������ϵ��������֤����
��3�����ݣ�2���Ľ�����ͼd�С�A+��B+��C+��D+��E+��F�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
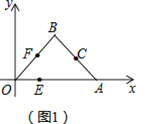
����Ŀ����֪���磨ͼ1������ƽ��ֱ�������У�A(12��0)��B(6��6)����CΪ�߶�AB���е㣬��D��ԭ��O���ڵ�C�Գƣ�
��1������ֱ�ߺ�Բ���ڣ�ͼ1����������D��λ�ã�������ͼ�ۼ������ж��ı���OBDA����״����˵�����ɣ�
��2���ڣ�ͼ1���У�����E�ӵ�O��������ÿ��1����λ���ٶ����߶�OA�˶��������Aʱֹͣ��ͬʱ������F�ӵ�O��������ÿ��a����λ���ٶ���OB��BD��DA�˶��������Aʱֹͣ�����˶���ʱ��Ϊt���룩��
�ٵ�t=4ʱ��ֱ��EFǡ��ƽ���ı���OBDA���������a��ֵ��
�ڵ�t=5ʱ��CE=CF����ֱ��д��a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
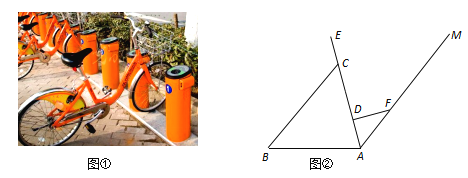
����Ŀ������̼����������ͬ�С��������꣬������еĹ������г���������д����˼���ķ��㣮ͼ���ǹ������г���ʵ��ͼ��ͼ���ǹ������г��ij���ʾ��ͼ����A��D��C��E��ͬһ��ֱ���ϣ�CD=30cm��DF=20cm��AF=25cm��FD��AE�ڵ�D������CE=15cm���ҡ�EAB=75�㣮
��1����AD�ij���
��2�����E��AB�ľ��룮���ο����ݣ�sin75���0.97��cos75���0.26��tan75���3.73��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���B��90����AC��60 cm����A��60������D�ӵ�C������CA������4 cm/����ٶ����A�����˶���ͬʱ��E�ӵ�A������AB������2 cm/����ٶ����B�����˶���������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������D��E�˶���ʱ����t��(0��t��15)������D��DF��BC�ڵ�F������DE��EF.

(1)�ı���AEFD�ܹ���Ϊ����������ܣ������Ӧ��tֵ��������ܣ���˵�����ɣ�
(2)��tΪ��ֵʱ����DEFΪֱ�������Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ˮ����ͨ��Դ�ͽ����Զ�����������ʱÿ��������10�������ȵ�100����ֹͣ���ȣ�ˮ�¿�ʼ�½�����ʱˮ�£������뿪������ʱ��min���ɷ�������ϵ��ֱ��ˮ�½���30������ˮ���ػ�����ˮ���ػ����Զ��������ظ������Զ���������ˮ��Ϊ30��ʱ����ͨ��Դ��ˮ��y��������ʱ�䣨min���Ĺ�ϵ��ͼ��Ϊ���������һ���¿�ʱ��8��45���ܺȵ�������50����ˮ�����ͨ��Դ��ʱ������ǵ��������
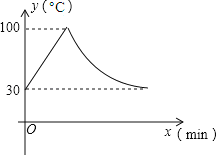
A��7��20 B��7��30 C��7��45 D��7��50
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
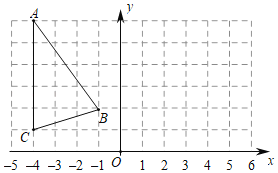
����Ŀ����ͼ��ƽ��ֱ������ϵxoy��A����4��6����B����1��2����C����4��1����
��1��������ABC����ֱ��x��1�ԳƵ�ͼ�Ρ�A1B1C1��д����A1B1C1����������ꣻ
��2������A1B1C1����ƽ��2����λ������ƽ�ƺ�ġ�A2B2C2����д����A2B2C2�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ϰ�ȥͼ�������г�����ij��ͼ�飬��һ���� 1200 Ԫ�������ɱ����� ÿ�� 10 Ԫ���ۣ��ܿ����꣮�ڶ��ι���ʱ��ÿ����Ľ��۱ȵ�һ������� 20%������1500 Ԫ������������ȵ�һ�ζ� 10 ����
��1�����һ�ι����ͼ�飬ÿ�����۶���Ԫ��
��2���ڶ��ι����ͼ�飬��ÿ�� 10 Ԫ�۳� 200 ��ʱ������������ʣ�µ�ͼ�齵�ۺ�ȫ�� �۳���Ҫʹ���������۵��������� 2100 Ԫ��ÿ�����ཱུ�۶���Ԫ��������=��������һ���ۣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com