
| A. | 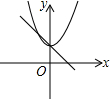 | B. | 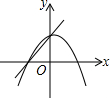 | C. | 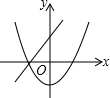 | D. | 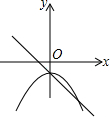 |
分析 可先根据一次函数的图象判断a、b的符号,再判断二次函数图象与实际是否相符,判断正误.
解答 解:A、由一次函数y=ax+b的图象可得:a<0,此时二次函数y=ax2+b的图象应该开口向下,故A错误;
B、由一次函数y=ax+b的图象可得:a>0,此时二次函数y=ax2+b的图象应该开口向上,顶点的故B错误;
C、由一次函数y=ax+b的图象可得:a>0,b>0,此时二次函数y=ax2+b的图象应该开口向上,交于y轴的正半轴,故C错误;
D、由一次函数y=ax+b的图象可得:a<0,b<0,此时二次函数y=ax2+b的图象应该开口向下,与直线交于y轴负半轴的同一点,故D正确;
故选:D.
点评 本题考查了二次函数的图象,应该熟记一次函数y=kx+b在不同情况下所在的象限,以及熟练掌握二次函数的有关性质:开口方向、对称轴、顶点坐标等.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
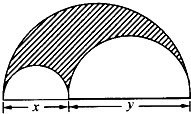 如图,一块半圆形钢板,从中挖去直径分别为x、y的两个半圆:
如图,一块半圆形钢板,从中挖去直径分别为x、y的两个半圆:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一条公路修到湖边时,需拐弯绕道而过,如果第一次拐的角∠A是100°第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是( )
如图,一条公路修到湖边时,需拐弯绕道而过,如果第一次拐的角∠A是100°第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是( )| A. | 120° | B. | 130° | C. | 140° | D. | 150° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
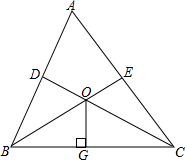 如图,△ABC中,∠BAC=60°,点D、E分别在AB、AC上,∠BCD=∠CBE=30°,BE、CD相交于点O,OG⊥BC于点G,求证:OE+OD=2OG.
如图,△ABC中,∠BAC=60°,点D、E分别在AB、AC上,∠BCD=∠CBE=30°,BE、CD相交于点O,OG⊥BC于点G,求证:OE+OD=2OG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com