
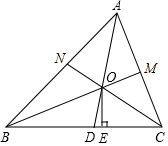
 如图,在△ABC中,三个内角的平分线AD、BM、CN交于点O,OE⊥BC于点E.
如图,在△ABC中,三个内角的平分线AD、BM、CN交于点O,OE⊥BC于点E.分析 (1)根据角平分线的定义可得∠BAO=∠CAO=$\frac{1}{2}$∠BAC、∠ABO=∠CBO=$\frac{1}{2}$∠ABC、∠ACO=∠BCO=$\frac{1}{2}$∠ACB,结合三角形的内角和可得∠ABO+∠BCO+∠CAO=$\frac{1}{2}$(∠ABC+∠ACB+∠BAC)=90°;
(2)根据三角形外角的性质可得∠BOD=∠ABO+∠BAO=90°-$\frac{1}{2}$∠ACB,由OE⊥BC结合三角形内角和可得出∠COE=90°-∠BCO=90°-$\frac{1}{2}$∠ACB,进而可得出∠BOD=∠COE,此题得解.
解答 解:(1)∵AD、BM、CN是△ABC三个内角的平分线,
∴∠BAO=∠CAO=$\frac{1}{2}$∠BAC,∠ABO=∠CBO=$\frac{1}{2}$∠ABC,∠ACO=∠BCO=$\frac{1}{2}$∠ACB,
∴∠ABO+∠BCO+∠CAO=$\frac{1}{2}$(∠ABC+∠ACB+∠BAC).
∵∠ABC+∠ACB+∠BAC=360°,
∴∠ABO+∠BCO+∠CAO=90°.
(2)∠BOD=∠COE,理由如下:
∵∠BOD是△ABO的外角,
∴∠BOD=∠ABO+∠BAO=$\frac{1}{2}$(∠ABC+∠BAC)=$\frac{1}{2}$(180°-∠ACB)=90°-$\frac{1}{2}$∠ACB.
∵OE⊥BC,
∴∠COE+∠BCO=90°,
∴∠COE=90°-∠BCO=90°-$\frac{1}{2}$∠ACB.
∴∠BOD=∠COE.
点评 本题考查了三角形内角和定理、角平分线以及三角形外角的性质,解题的关键是:(1)根据角平分线的定义找出∠ABO+∠BCO+∠CAO=$\frac{1}{2}$(∠ABC+∠ACB+∠BAC);(2)根据外角的性质结合三角形内角和找出∠BOD=90°-$\frac{1}{2}$∠ACB=∠COE.


 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
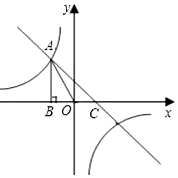 如图,已知反比例函数y=$\frac{k}{x}$(k<0)的图象经过点A(-$\sqrt{3}$,2),过点A作AB⊥x轴于点B,连结AO.
如图,已知反比例函数y=$\frac{k}{x}$(k<0)的图象经过点A(-$\sqrt{3}$,2),过点A作AB⊥x轴于点B,连结AO.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com