
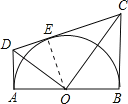
【题目】如图,AB为半圆O在直径,AD、BC分别切⊙O于A、B两点,CD切⊙O于点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2,④OD:OC=DE:EC,⑤OD2=DECD,正确的有( )

A.2个 B.3个 C.4个 D.5个
【答案】C
【解析】
试题分析:连接OE,由AD,DC,BC都为圆的切线,根据切线的性质得到三个角为直角,且利用切线长定理得到DE=DA,CE=CB,由CD=DE+EC,等量代换可得出CD=AD+BC,选项②正确;由AD=ED,OD为公共边,利用HL可得出直角三角形ADO与直角三角形EDO全等,可得出∠AOD=∠EOD,同理得到∠EOC=∠BOC,而这四个角之和为平角,可得出∠DOC为直角,选项①正确;由∠DOC与∠DEO都为直角,再由一对公共角相等,利用两对对应角相等的两三角形相似,可得出三角形DEO与三角形DOC相似,由相似得比例可得出OD2=DECD,选项⑤正确;由△AOD∽△BOC,可得![]() =
=![]() =
=![]() =
=![]() ,选项③正确;由△ODE∽△OEC,可得
,选项③正确;由△ODE∽△OEC,可得![]() ,选项④错误.
,选项④错误.
解:连接OE,如图所示:
∵AD与圆O相切,DC与圆O相切,BC与圆O相切,
∴∠DAO=∠DEO=∠OBC=90°,
∴DA=DE,CE=CB,AD∥BC,
∴CD=DE+EC=AD+BC,选项②正确;
在Rt△ADO和Rt△EDO中,![]() ,
,
∴Rt△ADO≌Rt△EDO(HL),
∴∠AOD=∠EOD,
同理Rt△CEO≌Rt△CBO,
∴∠EOC=∠BOC,
又∠AOD+∠DOE+∠EOC+∠COB=180°,
∴2(∠DOE+∠EOC)=180°,即∠DOC=90°,选项①正确;
∴∠DOC=∠DEO=90°,又∠EDO=∠ODC,
∴△EDO∽△ODC,
∴![]() =
=![]() ,即OD2=DCDE,选项⑤正确;
,即OD2=DCDE,选项⑤正确;
∵∠AOD+∠COB=∠AOD+∠ADO=90°,
∠A=∠B=90°,
∴△AOD∽△BOC,
∴![]() =
=![]() =
=![]() =
=![]() ,选项③正确;
,选项③正确;
同理△ODE∽△OEC,
∴![]() ,选项④错误;
,选项④错误;
故选C.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】利用网格画图:
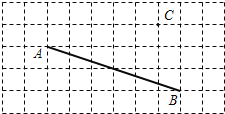
(1)过点C画AB的平行线CD;
(2)过点C画AB的垂线,垂足为E;
(3)线段CE的长度是点C到直线 的距离;
(4)连接CA、CB,在线段CA、CB、CE中,线段 最短,理由: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是( )
A.∠A=∠C﹣∠B
B.a:b:c=2:3:4
C.a2=b2﹣c2
D.a=![]() ,b=
,b=![]() ,c=1
,c=1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班有48位同学,在一次数学检测中,分数只取整数,统计其成绩,绘制出频数分布直方图(横半轴表示分数,把50.5分到100.5分之间的分数分成5组,组距是10分,纵半轴表示频数)如图所示,从左到右的小矩形的高度比是1:3:6:4:2,则由图可知,其中分数在70.5~80.5之间的人数是( )
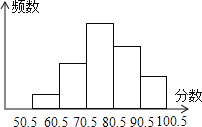
A.9 B.18 C.12 D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某粮店出售的三种品牌的面粉袋上,分别标有质量为(25±0.1)kg,(25±0.2)kg,(25±0.3)kg的字样,从中任意拿出两袋,它们的质量最多相差 ;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】

(1)如果点A表示的数-1,将点A向右移动4个单位长度,那么终点B表示的数是 ,A、B两点间的距离是 .
(2)如果点A表示的数2,将点A向左移动6个单位长度,再向右移动3个单位长度,那么终点B表示的数是 ,A、B两点间的距离是 .
(3)如果点A表示的数m,将点A向右移动n个单位长度,再向左移动p个单位长度,那么请你猜想终点B表示的数是 ,A、B两点间的距离是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com